| Главная » Статьи » Лекции |
1 вопрос. Нормальное распределение. 3 вопрос. Показательное распределение и его числовые характеристики.
1 вопрос. Нормальное распределение. Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью
где а - математическое ожидание, σ - среднее квадратическое отклонение Х.
Замечание 1. Общим называют нормальное распределение с произвольными параметрами а и σ (σ >0). Нормированным называют нормальное распределение с параметрами а=0 и σ =1. Например, если Х – нормальная величина с параметрами а и σ, то U = (X - a) / σ - нормированная нормальная величина, причем M(U)=0, σ(U)=1. Плотность нормированного распределения
Эта функция табулирована (см. приложение 1).
Замечание 2. Функция F(x) общего нормального распределения
а функция нормированного распределения
Функция F0(x) табулирована. Легко проверить, что
Замечание 3. Вероятность попадания нормированной нормальной величины Х в интервал (0, x) можно найти, пользуясь функцией Лапласа
Замечание 4. Учитывая, что
легко получить, что F0(x) = 0,5 + Ф(x) . Действительно, F0(x) = P(-∞ < X < x) = P(-∞ < X < 0) + P(0 < X < x) = 0,5 + Ф(x).
Вероятность того, что X примет значение, принадлежащее интервалу (α, β), равна
Преобразуя эту формулу, получим
где Функцию Лапласа находим по таблице (см. приложение 2).
Пример. Случайная величина X распределена по нормальному закону. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 30 и 10. Найти вероятность того, что X примет значение, принадлежащее интервалу (10, 50). Решение. Воспользуемся формулой (4.19). По условию, α=10, β=50, а=30, σ=10, следовательно,
По таблице приложения 2 находим Ф(2) = 0,4772. Отсюда искомая вероятность P(10 < X < 50) = 2 · 0,4772 = 0,9544.
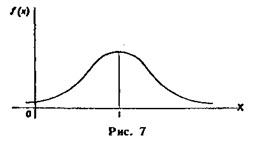
График плотности нормального распределения называют нормальной кривой (кривой Гаусса). Исследуем функцию
методами дифференциального исчисления.
Свойства нормальной кривой. 1. Очевидно, функция определена на всей оси х
2. При всех значениях х функция принимает положительные значения, т. е. нормальная кривая расположена над осью Ох. 3. Предел функции при неограниченном возрастании х по (абсолютной величине) равен нулю: 4. Исследуем функцию на экстремум. Найдем первую производную:
Легко видеть, что у'=0 при х = а, у'>0 при х<а, у' < 0 при х > а. Следовательно, при х = а функция имеет максимум равный 5. Разность х-а содержится в аналитическом выражении функции в квадрате, т. е. график функции симметричен относительно прямой х = а. 6. Исследуем функцию на точки перегиба. Найдем вторую производную:
Легко видеть, что при х=а+σ и х=а- σ вторая производная равна нулю, а при переходе через эти точки она меняет знак (в обеих этих точках значение функции равно
Как влияют на форму и расположение нормальной кривой значения параметров а и σ?
При а = 0 и σ = 1 нормальную кривую
3 вопрос. Показательное распределение и его числовые характеристики. Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины X, которое описывается плотностью
где λ - постоянная положительная величина.
Примером непрерывной случайной величины, распределенной по показательному закону, может служить время между появлениями двух последовательных событий простейшего потока (показательный закон надежности).
Функция распределения показательного закона:
Графики плотности и функции распределения показательного закона:
Пример 1. Написать плотность и функцию распределения показательного закона, если параметр λ = 8. Решение. Очевидно, искомая плотность распределения
Искомая функция распределения
Вероятность попадания в интервал (а, b) непрерывной случайной величины X, распределенной по показательному закону, P(a < X < b) = e-λa - e-λb. (4.22) Значения функции е-х находят по таблице.
Пример 2. Непрерывная случайная величина X распределена по показательному закону f(x) = 2e-2x при x ≥0; f(x) = 0 при x <0. Найти вероятность того, что в результате испытания X попадает в интервал (0,3, 1). Решение. По условию, λ = 2. Воспользуемся формулой (4.22): P(0,3 < X < 1) = e-(2·0,3) - e-(2·1) = e-0,6 - e-2 = 0,54881 - 0,13534 ≈ 0,41.
Числовые характеристики показательного распределения Математическое ожидание показательного распределения равно обратной величине параметра λ:
Дисперсия показательного распределения равна
Среднее квадратическое отклонение показательного распределения равно
Математическое ожидание и среднее квадратическое отклонение показательного распределения равны между собой.
Пример 3. Непрерывная случайная величина X распределена по показательному закону f(x) = 5e-5x при x ≥0; f(x) = 0 при x <0. Найти математическое ожидание, среднее квадратическое отклонение и дисперсию X. Решение. По условию, λ = 5. Следовательно,
| |
| Категория: Лекции | Просмотров: 4888 | |
| Всего комментариев: 0 | |
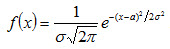 . (4.14)
. (4.14)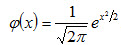 . (4.15)
. (4.15)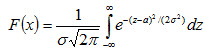 , (4.16)
, (4.16)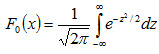 . (4.17)
. (4.17)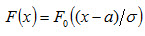 .
.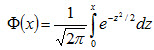 . Действительно,
. Действительно,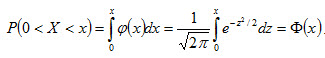 .
.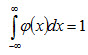 (свойство 2), и, следовательно, в силу симметрии φ(x) относительно нуля
(свойство 2), и, следовательно, в силу симметрии φ(x) относительно нуля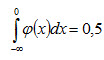 , а значит, и P (-∞ < X < 0) = 0,5,
, а значит, и P (-∞ < X < 0) = 0,5,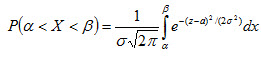 . (4.18)
. (4.18)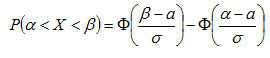 , (4.19)
, (4.19)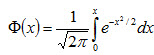 - функция Лапласа.
- функция Лапласа.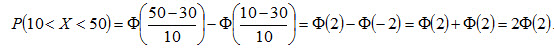 .
.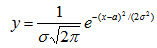
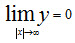 , т.е. ось Ох служит горизонтальной асимптотой графика.
, т.е. ось Ох служит горизонтальной асимптотой графика.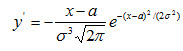 .
.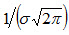 .
.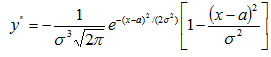 .
.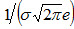 ). Таким образом, точки графика (а-σ,
). Таким образом, точки графика (а-σ, 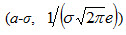 ) и (а+σ,
) и (а+σ, 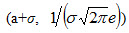 ) являются точками перегиба.
) являются точками перегиба.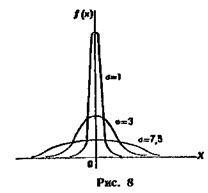
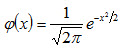 называют нормированной.
называют нормированной.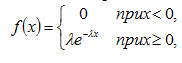 (4.21)
(4.21)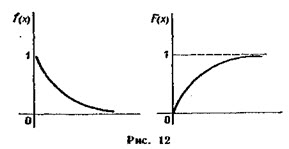
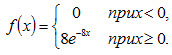
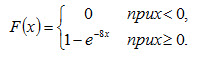
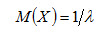 . (4.23)
. (4.23)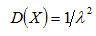 . (4.24)
. (4.24)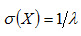 . (4.25)
. (4.25)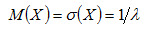
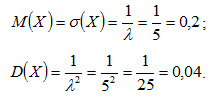 .
.