| Главная » Статьи » Лекции |
1 вопрос. Биномиальное распределение. 2 вопрос. Геометрическое распределение.
1 вопрос. Биномиальное распределение. Биномиальным называют закон распределения дискретной случайной величины X - числа появлений события в n независимых испытаниях, в каждом из которых вероятность появления события равна р; вероятность возможного значения X = k (числа k появлений события) вычисляют по формуле Бернулли: Pn(k) = Cknpkqn-k (2.22) Формула (2.22) является аналитическим выражением закона распределения дискретной случайной величины. Закон назван «биномиальным» потому, что правую часть равенства (2.22) можно рассматривать как общий член разложения бинома Ньютона:
Таким образом, первый член разложения рn определяет вероятность наступления рассматриваемого события n раз в n независимых испытаниях; второй член nрn-1q определяет вероятность наступления события n-1 раз;…; последний член qn определяет вероятность того, что событие не появится ни разу. Напишем биномиальный закон в виде таблицы:
Пример 1. Монета брошена 2 раза. Написать в виде таблицы закон распределения случайной величины X – числа выпадений «герба». Решение. Вероятность появления «герба» в каждом бросании монеты р=1/2, следовательно, вероятность непоявления «герба» q=1-1/2=1/2. При двух бросаниях монеты «герб» может появиться либо 2 раза, либо 1 раз, либо совсем не появиться. Таким образом, возможные значения X таковы: x1=2, x2=1, x3=0. Найдем вероятности этих возможных значений по формуле Бернулли:
Напишем искомый закон распределения:
Контроль: 0,25 + 0,5 + 0,25 = 1.
Математическое ожидание биномиального распределения равно произведению числа испытаний на вероятность появления события в одном испытании: M(x) = np. (3.7) Пример 2. Вероятность попадания в цель при стрельбе из орудия р=0,6. Найти математическое ожидание общего числа попаданий, если будет произведено 10 выстрелов. Решение. Попадание при каждом выстреле не зависит от исходов других выстрелов, поэтому рассматриваемые события независимы и, следовательно, искомое математическое ожидание M(x) = np = 10 · 0,6 = 6 (попаданий). Дисперсия биномиального распределения равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании: D(X) = npq. (3.8) Пример 3. Производятся 10 независимых испытаний, в каждом из которых вероятность появления события равна 0,6. Найти дисперсию случайной величины X – числа появления события в этих испытаниях. Решение. По условию п=10, р=0,6. Очевидно, вероятность непоявления события q = 1 - 0,6 = 0,4. Искомая дисперсия D(X) = npq = 10 · 0,6 · 0,4 = 2,4.
2 вопрос. Геометрическое распределение. Пусть производятся независимые испытания, в каждом из которых вероятность появления события А равна р (0< р <1) , следовательно, вероятность его непоявления q=1- р. Испытания заканчиваются, как только появится событие А. Таким образом, если событие А появилось в k–м испытании, то в предшествующих k-1 испытаниях оно не появилось. Обозначим через X дискретную случайную величину – число испытаний, которые нужно провести до первого появления события А. Очевидно, возможными значениями X являются натуральные числа: x1=1, x2=2, … Пусть в первых k-1 испытаниях событие А не наступило, а в k–м испытании появилось. Вероятность этого «сложного события», по теореме умножения вероятностей независимых событий, P(X=k) = qk-1p. (3.9) Полагая k=1, 2, … в формуле (3.9), получим геометрическую прогрессию с первым членом р и знаменателем q (0< q <1): р, qр, q2р, …, qk-1р, … (3.10) По этой причине распределение (3.9) называют геометрическим. Легко убедиться, что ряд (3.10) сходится и сумма его равна единице. Действительно, сумма ряда (3.10)
Пример. Из орудия производится стрельба по цели до первого попадания. Вероятность попадания в цель р=0,6. Найти вероятность того, что попадание произойдет при третьем выстреле. Решение. По условию р=0,6, q=0,4, k=3. Искомая вероятность по формуле (3.9) P = qk-1p = 0,42 · 0,6 = 0,096. | |||||||||||||||||||||||
| Категория: Лекции | Просмотров: 695 | |||||||||||||||||||||||
| Всего комментариев: 0 | |
 .
.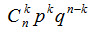
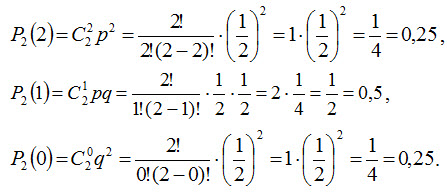 ,
,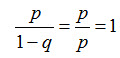 .
.