| Главная » Статьи » Лекции |
1 вопрос. Неравенство Чебышева. 4 вопрос. Центральная предельная теорема.
1 вопрос. Неравенство Чебышева. Для практики очень важно знание условий, при выполнении которых совокупное действие очень многих случайных причин приводит к результату, почти не зависящему от случая, так как позволяет предвидеть ход явлений. Эти условия указываются в теоремах, носящих общее название закона больших чисел. К ним относятся теоремы Чебышева и Бернулли. Теорема Чебышева является наиболее общим законом больших чисел, теорема Бернулли - простейшим.
Неравенство Чебышева справедливо для дискретных и непрерывных случайных величин. Рассмотрим дискретную случайную величину X, заданную таблицей распределения:
Поставим перед собой задачу оценить вероятность того, что отклонение случайной величины от ее математического ожидания не превышает по абсолютной величине положительного числа ε. Если ε достаточно мало, то мы оценим, таким образом, вероятность того, что X примет значения, достаточно близкие к своему математическому ожиданию. П. JI. Чебышев доказал неравенство, позволяющее дать интересующую нас оценку.
Неравенство Чебышева. Вероятность того, что отклонение случайной величины X от ее математического ожидания по абсолютной величине меньше положительного числа ε, не меньше, чем
Пример. Дискретная случайная величина X задана законом распределения
Используя неравенство Чебышева, оценить вероятность того, что |X - M(X)| < 0,2. Решение. Найдем математическое ожидание и дисперсию величины X: M(X) = 0,3 · 0,2 + 0,6 · 0,8 = 0,54; D(X) = M(X2) - [M(X)]2 = (0,32 · 0,2 + 0,62 · 0,8) - 0,542 = 0,09 · 0,2 + 0,36 · 0,8 - 0,2916 = 0,018+0,288 - 0,2916 = 0,0144. Воспользуемся неравенством Чебышева в форме (5.1).
Подставляя M(X) = 0,54, D(X) = 0,0144, ε = 0,2 окончательно получим
Замечание. Неравенство Чебышева имеет для практики ограниченное значение, поскольку часто дает грубую, а иногда и тривиальную (не представляющую интереса) оценку. Теоретическое же значение неравенства Чебышева весьма велико.
Теорема Чебышева. Если Х1, Х2, ..Хп, ...- попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают постоянного числа С), то, как бы мало ни было положительное число ε, вероятность неравенства
будет как угодно близка к единице, если число случайных величин достаточно велико. Другими словами, в условиях теоремы
Таким образом, теорема Чебышева утверждает, что если рассматривается достаточно большое число независимых случайных величин, имеющих ограниченные дисперсии, то почти достоверным можно считать событие, состоящее в том, что отклонение среднего арифметического случайных величин от среднего арифметического их математических ожиданий будет по абсолютной величине сколь угодно малым.
Пример. Последовательность независимых случайных величин Х1, Х2, ..., Хп, ... задана законом распределения
Применима ли к заданной последовательности теорема Чебышева? Решение. Для того чтобы к последовательности случайных величин была применима теорема Чебышева, достаточно, чтобы эти величины были попарно независимы, имели конечные математические ожидания и равномерно ограниченные дисперсии. Поскольку случайные величины независимы, то они подавно попарно независимы, т. е. первое требование теоремы Чебышева выполняется. Проверим, выполняется ли требование конечности математических ожиданий:
Таким образом, каждая случайная величина имеет конечное (равное нулю) математическое ожидание, т. е. второе требование теоремы выполняется. Проверим, выполняется ли требование равномерной ограниченности дисперсий. Напишем закон распределения X2n:
или, сложив вероятности одинаковых возможных значений,
Найдем математическое ожидание M(X2n):
Найдем дисперсию D(Xn), учитывая, что
Таким образом, дисперсии заданных случайных величин равномерно ограничены числом α2, т. е. третье требование выполняется. Итак, поскольку все требования выполняются, к рассматриваемой последовательности случайных величин теорема Чебышева применима
Выше, формулируя теорему Чебышева, мы предполагали, что случайные величины имеют различные математические ожидания. На практике часто бывает, что случайные величины имеют одно и то же математическое ожидание. Очевидно, что если вновь допустить, что дисперсии этих величин ограничены, то к ним будет применима теорема Чебышева. Обозначим математическое ожидание каждой из случайных величин через а; в рассматриваемом случае среднее арифметическое математических ожиданий, также равно а.
Теорема Чебышева (для частного случая). Если Х1, Х2, ..., Хп,... - попарно независимые случайные величины, имеющие одно и то же математическое ожидание а, и если дисперсии этих величин равномерно ограничены, то, как бы мало ни было число ε >0, вероятность неравенства
будет как угодно близка к единице, если число случайных величин достаточно велико.
Другими словами, в условиях теоремы будет иметь место равенство
На теореме Чебышева основан широко применяемый в статистике выборочный метод, суть которого состоит в том, что по сравнительно небольшой случайной выборке судят о всей совокупности (генеральной совокупности) исследуемых объектов. В качестве примера можно указать на определение качества зерна по небольшой его пробе. И в этом случае число наудачу отобранных зерен мало сравнительно со всей массой зерна, но само по себе оно достаточно велико.
Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины X по абсолютной величине меньше заданного положительного числа δ, т. е. требуется найти вероятность осуществления неравенства |X - a| < δ. Заменим это неравенство равносильным ему двойным неравенством
Пользуясь формулой (4.19), получим
Приняв во внимание равенство
(функция Лапласа - нечетная), окончательно имеем
В частности, при a = 0
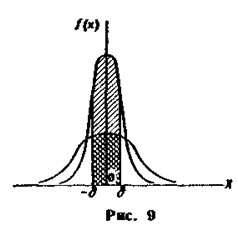
На рис. наглядно показано, что если две случайные величины нормально распределены и а = 0, то вероятность принять значение, принадлежащее интервалу (-δ, δ), больше у той величины, которая имеет меньшее значение σ. Этот факт полностью соответствует вероятностному смыслу параметра σ (σ есть среднее квадратическое отклонение; оно характеризует рассеяние случайной величины вокруг ее математического ожидания).
Замечание. Очевидно, события, состоящие в осуществлении неравенств |X - a| < δ и |X - a| ≥ δ, - противоположные. Поэтому, если вероятность осуществления неравенства |X - a| < δ равна р, то вероятность неравенства |X - a| ≥ δ равна 1—р.
Пример. Случайная величина X распределена нормально. Математическое ожидание и среднее квадратическое отклонение X соответственно равны 20 и 10. Найти вероятность того, что отклонение по абсолютной величине будет меньше трех. Решение. Воспользуемся формулой (5.4)
По условию, δ = 3, а = 20, σ =10. Следовательно,
По таблице приложения 2 находим Ф(0,3) = 0,1179. Искомая вероятность
Преобразуем формулу (5.4)
положив δ = σt. В итоге получим
Если t = 3 и, следовательно, σt = 3σ, то
т. е. вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973. Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна 0,0027. Это означает, что лишь в 0,27% случаев так может произойти. Такие события исходя из принципа невозможности маловероятных событий можно считать практически невозможными. В этом и состоит сущность правила трех сигм: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения. На практике правило трех сигм применяют так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле, выполняется, то есть основание предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально
4 вопрос. Центральная предельная теорема. Известно, что нормально распределенные случайные величины широко распространены на практике. Чем это объясняется? Ответ на этот вопрос был дан выдающимся русским математиком А. М. Ляпуновым (центральная предельная теорема). Центральная предельная теорема. Если случайная величина X представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то X имеет распределение, близкое к нормальному.
Пример. Пусть производится измерение некоторой физической величины. Любое измерение дает лишь приближенное значение измеряемой величины, так как на результат измерения влияют очень многие независимые случайные факторы (температура, колебания прибора, влажность и др.). Каждый из этих факторов порождает ничтожную «частную ошибку». Однако, поскольку число этих факторов очень велико, их совокупное действие порождает уже заметную «суммарную ошибку». Рассматривая суммарную ошибку как сумму очень большого числа взаимно независимых частных ошибок, мы вправе заключить, что суммарная ошибка имеет распределение, близкое к нормальному. Опыт подтверждает справедливость такого заключения.
Приведем формулировку центральной предельной теоремы, которая устанавливает условия, при которых сумма большого числа независимых слагаемых имеет распределение, близкое к нормальному. Пусть Х1, Х2, ..Xn,... - последовательность независимых случайных величин, каждая из которых имеет конечные математическое ожидание и дисперсию: M(Xk) = ak, D(Xk) = b2k. Введем обозначения:
Обозначим функцию распределения нормированной суммы через
Говорят, что к последовательности X1, Х2, ... применима центральная предельная теорема, если при любом x функция распределения нормированной суммы при n→∞ стремится к нормальной функции распределения:
В частности, если все случайные величины Х1, Х2,... одинаково распределены, то к этой последовательности применима центральная предельная теорема, если дисперсии всех величин Xi (I = 1, 2, …) конечны и отличны от нуля. А. М. Ляпунов доказал, что если для δ > 0 при n→∞ отношение Ляпунова
стремится к нулю (условие Ляпунова), то к последовательности Х1, Х2, ... применима центральная предельная теорема. Сущность условия Ляпунова состоит в требовании, чтобы каждое слагаемое суммы (Sn - An) / Bn оказывало на сумму ничтожное влияние. | |||||||||||||||||||||||||||||||||||||||
| Категория: Лекции | Просмотров: 2902 | |||||||||||||||||||||||||||||||||||||||
| Всего комментариев: 0 | |
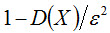 :
: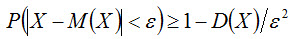 . (5.1)
. (5.1)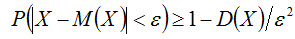 .
.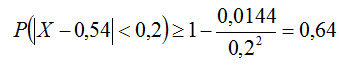 .
.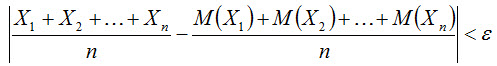
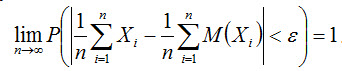 . (5.2)
. (5.2)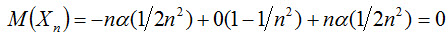 .
.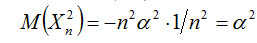 .
.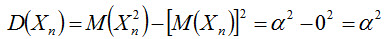 .
.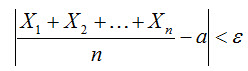
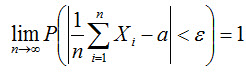 . (5.3)
. (5.3)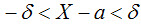 , или
, или 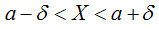 .
.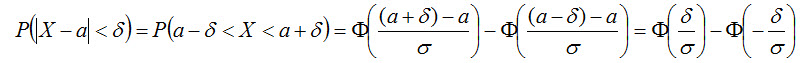 .
.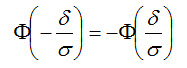
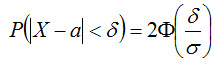 . (5.4)
. (5.4)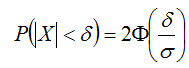 .
.
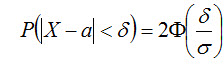 .
.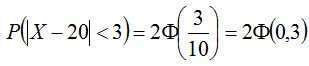 .
.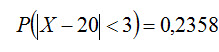 .
.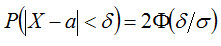 ,
,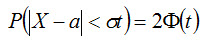 .
.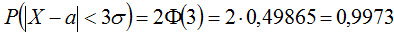 .
.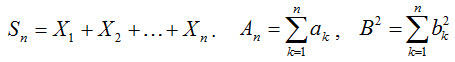 .
.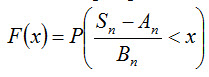 .
.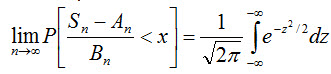 .
.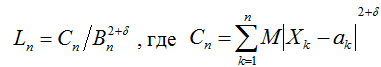 ,
,