| Главная » Статьи » Лекции |
1 вопрос. Числовые характеристики непрерывных случайных величин.
1 вопрос. Числовые характеристики непрерывных случайных величин. Пусть непрерывная случайная величина X задана плотностью распределения f(х). Допустим, что все возможные значения X принадлежат отрезку [а, b]. Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат отрезку [а, b] называют определенный интеграл
Если возможные значения принадлежат всей оси Ox, то
Все свойства математического ожидания, указанные для дискретных случайных величин, сохраняются и для непрерывных величин.
Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения. Если возможные значения X принадлежат отрезку [a, b], то
или
Если возможные значения принадлежат всей оси Ox, то
или
Все свойства дисперсии, указанные для дискретных случайных величин, сохраняются и для непрерывных величин.
Среднее квадратическое отклонение непрерывной случайной величины определяется, как и для величины дискретной, равенством
Пример 1. Найти математическое ожидание и дисперсию случайной величины X, заданной функцией распределения
Решение. Найдем плотность распределения:
Найдем математическое ожидание по формуле (4.7):
Найдем дисперсию по формуле (4.10):
| |
| Категория: Лекции | Просмотров: 315 | |
| Всего комментариев: 0 | |
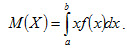 (4.7)
(4.7)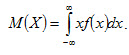 (4.8)
(4.8)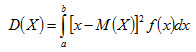 (4.9)
(4.9)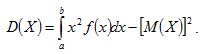 . (4.10)
. (4.10)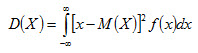 (4.11)
(4.11)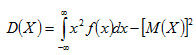 . (4.12)
. (4.12)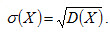 . (4.13)
. (4.13)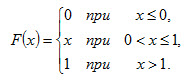
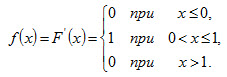
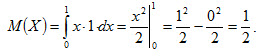 .
.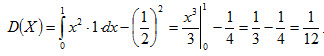 .
.