| Главная » Статьи » Лекции |
1 вопрос. Случайная величина.Дискретные случайные величины. 2 вопрос. Закон распределения вероятностей дискретной случайной величины.
1 вопрос. Случайная величина. Дискретные случайные величины. Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены. Случайные величины обозначаются прописными буквами X, Y, Z, а их возможные значения – соответствующими строчными буквами x, y, z. Например, если случайная величина X имеет три возможных значения, то они будут обозначены так: x1,x2,x3. Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным (множество всех возможных значений называют счетным).
Пример.Число родившихся мальчиков среди ста новорожденных есть случайная дискретная величина, которая имеет следующие возможные значения: 0, 1, 2, …, 100.
2 вопрос. Закон распределения вероятностей дискретной случайной величины. Закон распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями. Закон распределения дискретной случайной величины Xможет быть задан в виде таблицы, аналитически (в виде формулы) и графически. При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая – их вероятности:
Приняв во внимание, что в одном испытании случайная величина принимает одно и только одно возможное значение, заключаем, что события X=x1, X=x2, …, X=xn образуют полную группу; следовательно, сумма вероятностей этих событий, т.е. сумма вероятностей второй строки таблицы, равна единице: p1 + p2 +...+pn = 1 . Если множество возможных значений X бесконечно (счетно), то ряд p1 + p2 +... сходится и его сумма равна единице.
Пример 1. В денежной вещевой лотерее выпущено 100 билетов. Разыгрывается одни выигрыш в 50 руб. и десять выигрышей по 1 руб. Найти закон распределения случайной величиныX – стоимости возможного выигрыша для владельца одного лотерейного билета. Решение. Напишем возможные значенияX: x1=50,x2=1, x3=0. Вероятности этих возможных значений таковы:
Напишем искомый закон распределения:
Контроль: 0,01 + 0,1 + 0,89 = 1 .
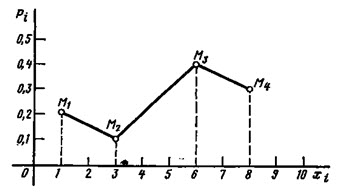
Закон распределения дискретной случайной величины можно изобразить графически, для чего в прямоугольной системе координат строят точки (xi;рi),а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения. Пример 2. Дискретная случайная величина Xзадана законом распределения:
Построить многоугольник распределения. Решение. Построим прямоугольную систему координат, причем по оси абсцисс будем откладывать возможные значения xi, а по оси ординат - соответствующие вероятности рi. Построим точки M1 (1;0,2), М2 (3;0,1),М3 (6;0,4) и М4(8;0,3). Соединив эти точки отрезками прямых, получим искомый многоугольник распределения.
| |||||||||||||||||||||||||||||
| Категория: Лекции | Просмотров: 1233 | |||||||||||||||||||||||||||||
| Всего комментариев: 0 | |
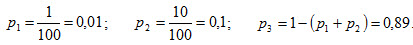 .
.