| Главная » Статьи » Лекции |
|
3 вопрос. Правила комбинаторики.
Пусть имеются четыре буквы А, В, С, D. Составив все комбинации только из двух букв, получим: АВ, AC, AD; ВА, ВС, BD; СА, СВ, CD; DA, DB, DC. Мы видим, что все полученные комбинации отличаются или буквами, или их порядком (комбинации ВА и АВ считаются различными). Комбинации из n элементов по т элементов, которые отличаются друг от друга или самими элементами или порядком элементов, называются размещениями. Размещения обозначаются символом Anm, где n — число всех имеющихся элементов, m — число элементов в каждой комбинации. При этом полагают, что т≤ п. Число размещений можно вычислить по формуле
т.е. число всех возможных размещений из n элементов по т равно произведению т последовательных целых чисел, из которых большее есть n
или по другой формуле (в факториальной форме)
Так, A24 = 4· 3 = 12, что совпадает с результатом приведенного примера: поскольку число строк соответствует числу всех имеющихся букв, т.е. n = 4, а число столбцов равно 3, всего имеется 12 различных комбинаций.
1. Вычислить:
2. Сколько двузначных чисел можно составить из пяти цифр 1, 2, 3, 4, 5 при условии, что ни одна из них не повторяется? Решение. Так как двузначные числа отличаются друг от друга или самими цифрами, или их порядком, то искомое количество равно числу размещений из пяти элементов по два.
3. Расписание одного дня состоит из 5 уроков. Определить число вариантов расписания при выборе из 11 дисциплин.
Решение. Каждый вариант расписания представляет набор 5 дисциплин из 11, отличающийся от других вариантов, как составом дисциплин, так и порядком их следования (или и тем и другим), т.е. является размещением из 11 элементов по 5. Число вариантов расписаний находим по формуле (3).
Сочетаниями называются все возможные комбинации из п элементов по т, которые отличаются друг от друга по крайней мере хотя бы одним элементом (здесь m и п — натуральные числа, причем т≤ п ). Так, из четырех различных букв А, В, С, D можно составить следующие комбинации, отличающиеся друг от друга хотя бы одним элементом: АВ, AC, AD, ВС, BD, CD. Значит, число сочетаний из четырех элементов по два равно 6. Это кратко записывается так: C 24 = 6. В каждой комбинации сделаем перестановки элементов: АВ, AC, AD, ВС, BD, CD, ВА, СА, DA, CB, DB, DC. В результате мы получили размещения из четырех элементов по два. Следовательно,
Следовательно, в общем случае число из п элементов по т равно числу размещений из п элементов по т, деленному на число перестановок из т элементов: В общем случае число из т элементов по п равно числу по п, деленному на число перестановок из п элементов:
Используя для чисел размещений и перестановок факториальные формулы, получим формулу числа сочетаний в виде
4. Вычислить:
Отметим основные свойства числа сочетаний:
Свойство числа сочетаний (формула 7) позволяет упростить нахождение числа сочетаний из п элементов по m, когда m превосходит 5. Сколькими способами можно выбрать трех дежурных, если в классе 30 учащихся?
6. В шахматном турнире участвуют 16 человек. Сколько партий должно быть сыграно в турнире, если между любыми двумя участниками должна быть сыграна одна партия? Решение. Каждая партия играется двумя участниками из 16 и отличается от других только составом пар участников, т.е. представляет собой сочетание из 16 элементов по 2. Их число находим по формуле (6):
3 вопрос. Правила комбинаторики. Пусть Ai (i=1, 2, … n) – элементы конечного множества. При решении задач комбинаторики используют следующие правила.
Правило суммы. Если элемент A1 может быть выбран n1 способами, элемент A2 – другими n2 способами, A3 - отличными от первых двух n3 способами и т.д., Ak - nk способами, отличными от первых (k-1), то выбор одного из элементов: или A1, или A2, … или Ak может быть осуществлен n1 + n2 + ...+ nk способами.
7. В ящике 300 деталей. Известно, что 150 из них – 1-го сорта. 120 – 2-го, а остальные – 3-го сорта. Сколько существует способов извлечения из ящика одной детали 1-го или 2-го сорта? Решение. Деталь 1-го сорта может быть извлечена n1 = 150 способами, 2-го - n2 = 120 способами. По правилу суммы существует n1 + n2 = 150 + 120 = 270 способов извлечения одной детали 1-го или 2-го сорта.
Правило произведения. Если элемент A1 может быть выбран n1 способами, после каждого такого выбора элемент A2 может быть выбран n2 способами и т.д., после каждого (k-1) выбора элемент Ak может быть выбран nk способами, то выбор всех элементов A1, A2, … или Ak в указанном порядке может быть осуществлен n1·n2·...nk способами.
8. В группе 30 человек. Необходимо выбрать старосту, его заместителя и профорга. Сколько существует способов это сделать? Решение. Староста может быть выбран любой из 30 учащихся, его заместителем – любой из оставшихся 29, а профоргом - любой из оставшихся 28 учащихся, т.е. n1 = 30, n2 = 29, n3 = 28. По правилу произведения общее число способов выбора старосты, его заместителя и профорга равно n1·n2·n3 = 30 · 29 · 28 = 24360 способов. | |
| Категория: Лекции | Просмотров: 2010 | |
| Всего комментариев: 0 | |
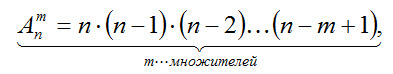 (1.3)
(1.3)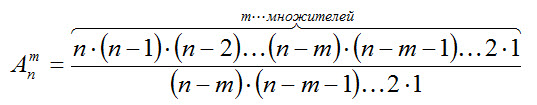
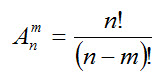 . (1.4)
. (1.4)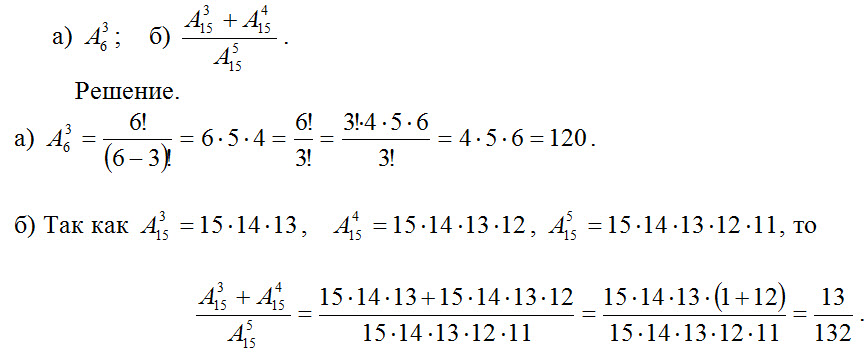
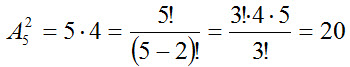 .
.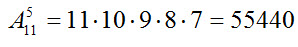 .
.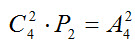 , откуда
, откуда 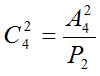 .
.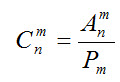 . (1.5)
. (1.5)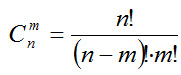 . (1.6)
. (1.6)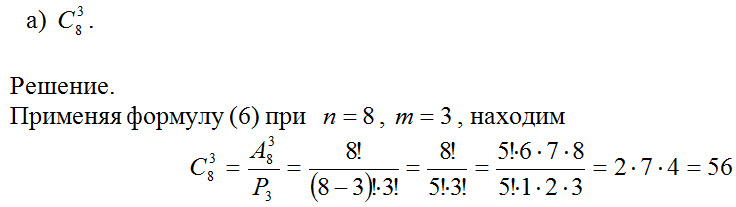 .
.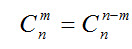 , (1.7)
, (1.7)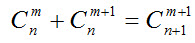 . (1.8)
. (1.8)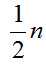 .
.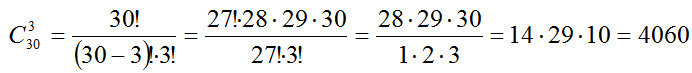 .
.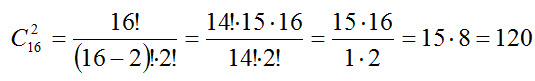 .
.