| Главная » Статьи » Лекции |
1 вопрос. Вероятность появления хотя бы одного события. 2 вопрос. Теорема сложения вероятностей совместных событий. 3 вопрос. Формула полной вероятности. 4 вопрос. Вероятность гипотез. Формула Байеса.
1 вопрос. Вероятность появления хотя бы одного события. Пусть в результате испытания могут появиться n событий, независимых в совокупности, либо некоторые из них (в частности, только одно или ни одного), причем вероятности появления каждого из событий известны. Теорема. Вероятность появления хотя бы одного из событий А1, А2,..., Аn, независимых в совокупности, равна разности между единицей и произведением вероятности противоположных событий P(A) = 1 - q1 q2 ... qn (2.14) Если события А1, А2,..., Аn имеют одинаковую вероятность, равную p, то вероятность появления хотя бы одного из этих событий P(A) = 1 - qn (2.15)
Пример 1. Вероятности попадания в цель при стрельбе из трех орудий таковы: p1=0,8; p2=0,7; p3=0,9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий. Решение. Вероятности попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события А1 (попадание первого орудия), А2 (попадание второго орудия) и А3 (попадание третьего орудия) независимы в совокупности. Вероятности событий, противоположных событиям А1, А2 и А3 (т.е. вероятности промахов), соответственно равны: q1 = 1 - p1 = 1 - 0,8 = 0,2 q2 = 1 - p2 = 1 - 0,7 = 0,3 q3 = 1 - p3 = 1 - 0,9 = 0,1 Искомая вероятность P(A) = 1 - q1 q2 q3 = 1 - 0,2 · 0,3 · 0,1 = 1 - 0,006 = 0,994
2 вопрос. Теорема сложения вероятностей совместных событий. Два события называют совместными, если появление одного из них не исключает появления другого в одном и том же испытании.
Пример 1. А-появление четырех очков при бросании игральной кости; В-появление четного числа очков. События А и В - совместные.
Пусть события А и В совместны, причем даны вероятности этих событий и вероятность их совместного появления. Найти вероятность события А+В, состоящего в том, что появится хотя бы одно из событий А и В.
Теорема сложения вероятностей совместных событий. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событии без вероятности их совместного появления: P(A+B) = P(A) + P(B) - P(AB) (2.16) Замечание 1. При использовании формулы (2.16) следует иметь в виду, что события А и В могут быть как независимыми, так и зависимыми. Для независимых событий P(A+B) = P(A) + P(B) - P(A) · P(B) (2.17) для зависимых событий P(A+B) = P(A) + P(B) - P(A) · PA(B) (2.18) Замечание 2. Если события А и В несовместны, то их совмещение есть невозможное событие и, следовательно, P(AB) = 0 . Формула (2.16) для несовместных событий принимает вид P(A+B) = P(A) + P(B) Мы вновь получили теорему сложения для несовместных событий. Таким образом, формула (2.16) справедлива как для совместных, так и для несовместных событий.
Пример 2. Вероятности попадания в цель при стрельбе первого и второго орудий соответственно равны: p1=0,7; p2=0,8. Найти вероятность попадания при одном залпе (из обоих орудий) хотя бы одним из орудий. Решение. Вероятности попадания в цель каждым из орудий не зависит от результата стрельбы из другого орудия, поэтому события А (попадание первого орудия) и В (попадание второго орудия) независимы. Вероятность события АВ (оба орудия дали попадание) P(AB) = P(A) · P(B) = 0,7 · 0,8 = 0,56 Искомая вероятность P(A+B) = P(A) + P(B) - P(AB) = 0,7 + 0,8 - 0,56 = 0,94
3 вопрос. Формула полной вероятности. Пусть А событие может наступать при условии появления одного из несовместных событий В1,B2,..., Вn, которые образуют полную группу. Пусть известны вероятности этих событий и условные вероятности РВ1(А), РВ2(А),…, РВn(А)события А. Найти вероятность события А. Теорема. Вероятность события А,которое может наступить лишь при условии появления одного из несовместных событий В1, B2,..., Вn,образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А: P(A) = P(B1) · PB1(A) + P(B2)· PB2(A) + ... P(Bn)· PBn(A) (2.19) Эту формулу называют «формулой полной вероятности».
Пример 1. Имеется два набора деталей. Вероятность того, что деталь первого набора стандартная, равна 0,8, а второго – 0,9. Найти вероятность того, что взятая наудачу деталь (из наудачу взятого набора) – стандартная. Решение. Обозначим через А событие «извлеченная деталь стандартна». Деталь может быть извлечена либо из первого набора (событие B1), либо из второго (событие B2). Вероятность того, что деталь вынута из первого набора,
Вероятность того, что деталь вынута из второго набора,
Условная вероятность того, что из первого набора будет извлечена стандартная деталь, PB1(A) = 0,8 Условная вероятность того, что из второго набора будет извлечена стандартная деталь, PB2(A) = 0,9 Искомая вероятность того, что извлеченная наудачу деталь – стандартная, по формуле полной вероятности равна P(A) = P(B1) · PB1(A) + P(B2)· PB2(A) = 0,5 · 0,8 + 0,5 · 0,9 = 0,85
4 вопрос. Вероятность гипотез. Формула Байеса. Пусть событие А может наступить лишь при условии появления одного из несовместных событий (гипотез) В1, B2,…, Вn,образующих полную группу. Поскольку заранее не известно, какое из этих событий наступит, их называют гипотезами. Вероятность появления события А определяется по формуле полной вероятности (2.19) P(A) = P(B1) · PB1(A) + P(B2)· PB2(A) + ... P(Bn)· PBn(A) Допустим, что произведено испытание, в результате которого появилось событие А. Поставим своей задачей определить, как изменились (в связи с тем, что событие А уже наступило) вероятности гипотез. Другими словами, будем искать условные вероятности PA(B1), PA(B2), ..., PA(Bn) Найдем сначала условную вероятность PA(B1) . По теореме умножения (2.7) имеем P(AB1) = P(A) · PA(B1) = P(B1) · PB1(A) Отсюда
Заменив здесь P(A) по формуле умножения (2.19), получим
Аналогично выводятся формулы, определяющие условные вероятности остальных гипотез, т.е. условная вероятность любой гипотезы Bi(i= 1, 2, …, n) может быть вычислена по формуле
Полученные формулы называют формулами Байеса (по имени английского математика, который их вывел; опубликованы в 1764 г.). Формулами Байеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.
Пример 1. Детали, изготовляемые цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Вероятность того, что деталь попадает к первому контролеру, равна 0,6, а ко второму – 0,4. Вероятность того, что годная деталь будет признана стандартной первым контролером, равна 0,94, а вторым – 0,98. Годная деталь при проверке была признана стандартной. Найти вероятность того, что эту деталь проверил первый контролер.
Решение. Обозначим через А событие, состоящее в том, что годная деталь признана стандартной. Можно сделать два предположения:
Искомую вероятность того, что деталь проверил первый контролер, найдем по формуле Бейеса:
По условию задачи имеем: P(B1) = 0,6 (вероятность того, что деталь попадет к первому контролеру); P(B2) = 0,4 (вероятность того, что деталь попадет ко второму контролеру); PB1(A) = 0,94 (вероятность того, что деталь годная будет признана первым контролером стандартной); PB2(A) = 0,98 (вероятность того, что деталь годная будет признана вторым контролером стандартной). Искомая вероятность
Как видно, до испытания вероятность гипотезы В1 равнялась 0,6, а после того, как стал известен результат испытания, вероятность этой гипотезы (точнее, условная вероятность) изменилась и стала равна 0,59. Таким образом, использование формулы Бейеса позволило переоценить вероятность рассматриваемой гипотезы.
| |
| Категория: Лекции | Просмотров: 649 | |
| Всего комментариев: 0 | |
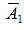 ,
, 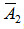 , …
, … 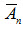 :
: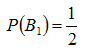
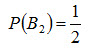
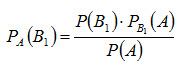
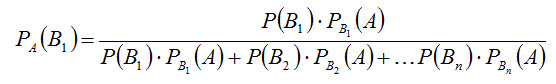 (2.20)
(2.20)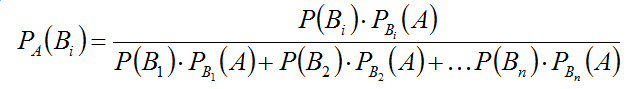 (2.21)
(2.21)