| Главная » Статьи » Лекции |
1 вопрос. Математическое ожидание дискретной случайной величины и её свойства. 2 вопрос. Дисперсия дискретной случайной величины и её свойства. 3 вопрос. Среднее квадратическое отклонение дискретной случайной величины.
1 вопрос. Математическое ожидание дискретной случайной величины и её свойства. Закон распределения полностью характеризует случайную величину. Часто закон распределения неизвестен и тогда выгоднее пользоваться числами, которые описывают случайную величину суммарно; такие числа называют числовыми характеристиками случайной величины. К числу важных числовых характеристик относится математическое ожидание. Характеристикой среднего значения дискретной случайной величины служит математическое ожидание. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности: M(X) = x1p1 + x2p2 + ... xnpn , (3.1) где X – дискретная случайная величина xi – значения дискретной случайной величины рi – вероятности дискретной случайной величины
Если дискретная случайная величина X принимает счетное множество возможных значений, то
причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.
Пример 1. Найти математическое ожидание дискретной случайной величины X, зная закон её распределения:
Решение. Искомое математическое ожидание равно сумме произведений всех возможных значений случайной величины на их вероятности, т.е. формула (3.1): M(X) = 3 · 0,1 + 5 · 0,6 + 2 · 0,3 = 3,9 . Математическое ожидание числа появления события в одном испытании равно вероятности этого события: M(X) = p . (3.3)
Свойства математического ожидания Свойство 1. Математическое ожидание постоянной величины равно самой постоянной: M(C) = C . Свойство 2. Постоянный множитель можно выносить за знак математического ожидания: M(CX) = CM(X) . Свойство 3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий: M(XY) = M(X) · M(Y) . Следствие. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий: M(X1X2...Xn) = M(X1) · M(X2) ·... M(Xn) . Пример 2. Независимые случайные величины X и Y заданы законами распределения:
Найти математическое ожидание дискретной случайной величины XY. Решение. Найдем математические ожидания каждой из данных величин: M(X) = 5 · 0,6 + 2 · 0,1 + 4 · 0,3 = 4,4 ; M(Y) = 7 · 0,8 + 9 · 0,2 = 7,4 . Случайные величины X и Y независимые, поэтому искомое математическое ожидание M(XY) = M(X) · M(Y) = 4,4 · 7,4 = 32,56.
Свойство 4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых: M(X+Y) = M(X) + M(Y) . Следствие. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий слагаемых: M(X1+X2+...Xn) = M(X1) + M(X2) +...+ M(Xn) . Пример 3. Найти математическое ожидание суммы числа очков, которые могут выпасть при бросании двух игральных костей. Решение. Обозначим число очков, которое может выпасть на первой кости, через X и на второй – через Y. Возможные значения этих величин одинаковы и равны 1, 2, 3, 4, 5 и 6, причем вероятность каждого из этих значений равна 1/6. Найдем математическое ожидание числа очков, которые могут выпасть на первой кости:
Очевидно, что и Искомое математическое ожидание
2 вопрос. Дисперсия дискретной случайной величины и её свойства. Математическое ожидание полностью случайную величину не характеризует. Поэтому наряду с математическим ожиданием вводят и другие числовые характеристики: дисперсию и среднее квадратическое отклонение. Пусть X – случайная величина и M(X) – математическое ожидание. Отклонением называют разность между случайной величиной и ее математическим ожиданием: X - M(X) . Свойство отклонения. Математическое ожидание отклонения равно нулю: M[X - M(X)] = 0 . На практике часто требуется оценить рассеяние возможных значений случайной величины вокруг ее математического ожидания (среднего значения), которую называют дисперсией. Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: D(X) = M[X - M(X)]2 . (3.4) Для вычисления дисперсии удобно пользоваться следующей теоремой. Теорема. Дисперсия равна разности между математически ожиданием квадрата случайной величины X и квадратом ее математического ожидания: D(X) = M(X2) - [M(X)]2 . (3.5) Пример 1. Найти дисперсию случайной величины X, которая задана следующим законом распределения:
Решение. Найдем математическое ожидание M (X): M(X) = 2 · 0,1 + 3 · 0,6 + 5 · 0,3 = 3,5 . Напишем закон распределения случайной величины X2:
Найдем математическое ожидание M (X2): M(X2) = 4 · 0,1 + 9 · 0,1 + 25 · 0,3 = 13,3 . Искомая дисперсия D(X) = M(X2) - [M(X)]2 = 13,3 - (3,5)2 = 13,3 - 12,25 = 1,05 .
Дисперсия обладает следующими свойствами. Свойство 1. Дисперсия постоянной величины равна нулю: D(C) = 0 . Свойство 2. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: D(CX) = C2D(X) . Свойство 3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин: D(X+Y) = D(X) + D(Y). Следствие 1. Дисперсия суммы нескольких взаимно независимых случайных величин равно сумме дисперсий этих величин: D(X1+X2+...+Xn) = D(X1) + D(X2) + ... + D(Xn). Следствие 2. Дисперсия суммы постоянной величины и случайной равна дисперсии случайной величины: D(C+X) = D(X) . Свойство 4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий: D(X-Y) = D(X) + D(Y) .
3 вопрос. Среднее квадратическое отклонение дискретной случайной величины. Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения кроме дисперсии служит и среднее квадратическое отклонение. Средним квадратическим отклонением случайной величины X называют квадратный корень из дисперсии:
Дисперсия имеет размерность равную квадрату размерности случайной величины. Так как среднее квадратическое отклонение равно квадратному корню из дисперсии, то размерность σ(X) совпадает с размерностью X. Поэтому в тех случаях, когда желательно, чтобы оценка рассеяния имела размерность случайной величины, вычисляют среднее квадратическое отклонение, а не дисперсию. Например, если X выражается в линейных метрах, то σ(X) будет выражаться также в линейных метрах, а D(X) - в квадратных метрах.
Пример. Случайная величина X задана законом распределения:
Найти среднее квадратическое отклонение σ(X) . Решение. Найдем математическое ожидание X: M(X) = 2 · 0,1 + 3 · 0,4 + 10 · 0,5 = 6,4 . Найдем математическое ожидание X2: M(X2) = 22 · 0,1 + 32 · 0,4 + 102 · 0,5 = 4 · 0,1 + 9 · 0,4 + 100 · 0,5 = 0,4 + 3,6 + 50 = 54. Найдем дисперсию: D(X) = M(X2) - [M(X)]2 = 54 - 6,42 = 54 - 40,96 = 13,04. Искомое среднее квадратическое отклонение
| |||||||||||||||||||||||||||||||||||||||||||||||||
| Категория: Лекции | Просмотров: 633 | |||||||||||||||||||||||||||||||||||||||||||||||||
| Всего комментариев: 0 | |
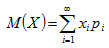 , (3.2)
, (3.2)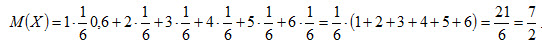 .
.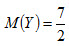 .
.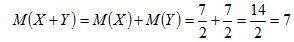 .
.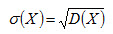 . (3.6)
. (3.6)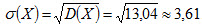 .
.