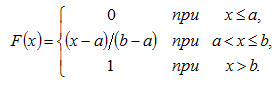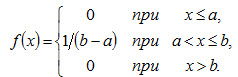| Главная » Статьи » Лекции |
1 вопрос. Определение функции распределения. 2 вопрос. Определение плотности распределения. 3 вопрос. Закон равномерного распределения вероятностей.
1 вопрос. Определение функции распределения. Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений непрерывной случайной величины бесконечно. Рассмотрим случайную величинуX, возможные значения которой сплошь заполняют интервал (a,b). Пусть x– действительное число. Вероятность события, состоящего в том, что X примет значение, меньшее x, т.е. вероятность события X<x, обозначим через F(x). Разумеется, если x изменяется, то, вообще говоря, изменяется и F(x), т.е. F(x) – функция от x. Функцией распределения называют функцию F(х),определяющую вероятность того, что случайная величина X в результате испытания примет значение, меньшее х, т.е. F(X) = P(X<x) . (4.1) Геометрически это равенство можно истолковать так: F(x)есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки x. Иногда вместо термина «функция распределения» используют термин «интегральная функция». Точное определение непрерывной случайной величины: случайную величину называют непрерывной, если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.
Свойства функции распределения Свойство 1. Значения функции распределения принадлежат отрезку [0; 1]: 0 ≤ F(X) ≤ 1 . Свойство 2. F(x) - неубывающая функция, т.е. F(x2) ≥ F(x1) , если x2>x1. F(x2) - F(x1) = P(x1 ≤ X ≤ x2). (4.2) Следствие 1. Вероятность того, что случайная величина X примет значение, заключенное в интервале (а,b), равна приращению функции распределения на этом интервале: P(a ≤ X ≤ b) = F(b) - F(a) . (4.3) Это важное следствие вытекает из формулы (4.2), если положить x2=b и x1=a. Следствие 2. Вероятность того, что непрерывная случайная величина X примет одно определенное значение, равна нулю. P(X=x1) = 0 . Свойство 3. Если возможные значения случайной величины принадлежат интервалу (а, b), то
Следствие. Если возможные значения непрерывной случайной величины расположены на всей осиx, то справедливы следующие предельные соотношения:
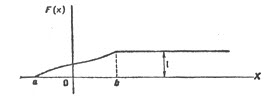
График функции распределения расположен в полосе, ограниченной прямымиy=0,y=1 (первое свойство). При возрастании xв интервале(а, b), в котором заключены все возможные значения случайной величины, график «подымается вверх» (второе свойство). При x≤ а ординаты графика равны нулю; при х ≥ b ординаты графика равны единице (третье свойство).
Пример.Случайная величина задана функцией распределения
Найти вероятность того, что в результате испытания Xпримет значение, принадлежащее интервалу (0, 2). Решение. По формуле (4.3) P(0<X<2) = F(2) - F(0) . Так как на интервале (0, 2), по условию, F(x) = x/4 + 1/4 , то Итак,
2 вопрос. Определение плотности распределения. Способ задания непрерывной случайной величины с помощью функции распределения не является единственным.Непрерывную случайную величину можно также задавать, используя другую функцию, которую называют плотностью распределения или плотностью вероятности (иногда ее называют дифференциальной функцией). Плотностью распределения вероятностей непрерывной случайной величины X называют функцию f(х) - первую производную от функции распределения F(x): f(x) = F(x)' . (4.4) Заметим, что для описания распределения вероятностей дискретной случайной величины плотность распределения неприменима. Зная плотность распределения, можно вычислить вероятность того, что непрерывная случайная величина примет значение, принадлежащее заданному интервалу. Вычисление основано на следующей теореме.
Теорема. Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (а, b), равна определенному интегралу от плотности распределения, взятому в пределах от а до b:
Геометрически полученный результат можно истолковать так: вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (а, b), равна площади криволинейной трапеции, ограниченной осью Ох, кривой распределения f(х) и прямыми х = а и х = b. Замечание. В частности, если f(х)- четная функция и концы интервала симметричны относительно начала координат, то
Пример 1. Задана плотность вероятности случайной величины X
Найти вероятность того, что в результате испытания X примет значение, принадлежащее интервалу (0,5; 1). Решение. Искомая вероятность
Зная плотность распределенияf(х),можно найти функцию распределенияF(х) по формуле
Свойства плотности распределения Свойство 1. Плотность распределения - неотрицательная функция: f(x) ≥ 0. Геометрически это свойство означает, что точки, принадлежащие графику плотности распределения, расположены либо над осью Ох,либо на этой оси. График плотности распределения называют кривой распределения.
Свойство 2. Несобственный интеграл от плотности распределения в пределах от -∞ до ∞ равен единице:
Геометрически это означает, что вся площадь криволинейной трапеции, ограниченной осью Ох и кривой распределения, равна единице.
Пример 2. Найти функцию распределения по данной плотности распределения:
Построить график найденной функции. Решение. Воспользуемся формулой (4.6). Если х ≤ а,,то f(x)=0,следовательно, F(x) = 0. Если а < х ≤ b,то f(x) = 1 / (b - а), следовательно,
Если х>b,то
Итак, искомая функция распределения
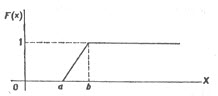
График этой функции:
3 вопрос. Закон равномерного распределения вероятностей. При решении задач, которые выдвигает практика, приходится сталкиваться с различными распределениями непрерывных случайных величин. Плотности распределений непрерывных случайных величин называют также законами распределений. Часто встречаются законы равномерного, нормального и показательного распределений. Распределение вероятностей называют равномерным,если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение. Пример равномерно распределенной непрерывной случайной величины.Шкала измерительного прибора проградуирована в некоторых единицах. Ошибку при округлении отсчета до ближайшего целого деления можно рассматривать как случайную величину X, которая может принимать с постоянной плотностью вероятности любое значение между двумя соседними целыми делениями. Таким образом, X имеет равномерное распределение. Плотность вероятности равномерного распределения
График плотности равномерного распределения:
| |
| Категория: Лекции | Просмотров: 1803 | |
| Всего комментариев: 0 | |
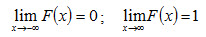 .
.
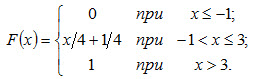
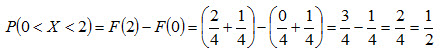 .
.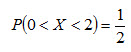 .
.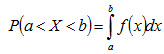 . (4.5)
. (4.5)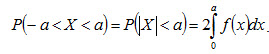 .
.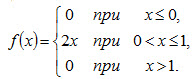
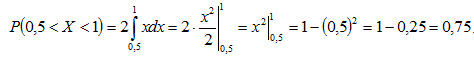 .
.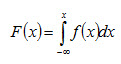 . (4.6)
. (4.6)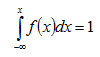 .
.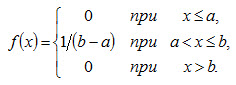
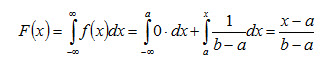 .
.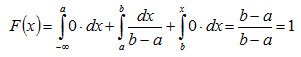 .
.