| Главная » Статьи » Лекции |
1 вопрос. Статистическая гипотеза. Нулевая и конкурирующая, простая и сложная гипотезы. 2 вопрос. Статистический критерий проверки нулевой гипотезы. Наблюдаемое значение критерия.
1 вопрос. Статистическая гипотеза. Нулевая и конкурирующая, простая и сложная гипотезы. Часто необходимо знать закон распределения генеральной совокупности. Если закон распределения неизвестен, но имеются основания предположить, что он имеет определенный вид (назовем его А), выдвигают гипотезу. Виды гипотез:
Статистической называют гипотезу о виде неизвестного распределения, или о параметрах известных распределений. Например, статистическими являются гипотезы:
В первой гипотезе сделано предположение о виде неизвестного распределения, во второй - о параметрах двух известных распределений. Наряду с выдвинутой гипотезой рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза будет отвергнута, то имеет место противоречащая гипотеза. По этой причине эти гипотезы целесообразно различать. Нулевой (основной) называют выдвинутую гипотезу Н0. Конкурирующей (альтернативной) называют гипотезу Hl, которая противоречит нулевой. Например, если нулевая гипотеза состоит в предположении, что математическое ожидание а нормального распределения равно 10, то конкурирующая гипотеза, в частности, может состоять в предположении, что а ≠ 10. Коротко это записывают так: Н0: а= 10; Н1: а ≠ 10. Различают гипотезы, которые содержат только одно и более одного предположений. Простой называют гипотезу, содержащую только одно предположение. Например, если λ - параметр показательного распределения, то гипотеза H0: λ= 5 - простая. Гипотеза H0:: математическое ожидание нормального распределения равно 3 (σ известно) - простая. Сложной называют гипотезу, которая состоит из конечного или бесконечного числа простых гипотез. Например, сложная гипотеза H: λ > 5 состоит из бесчисленного множества простых вида Нi:λ = bi где bi — любое число, большее 5. Гипотеза H0: математическое ожидание нормального распределения равно 3 (σ неизвестно) - сложная.
Ошибки первого и второго рода Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость ее проверки. Поскольку проверку производят статистическими методами, ее называют статистической. В итоге статистической проверки гипотезы в двух случаях может быть принято неправильное решение, т. е. могут быть допущены ошибки двух родов. Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза. Подчеркнем, что последствия этих ошибок могут оказаться весьма различными. Например, если отвергнуто правильное решение «продолжать строительство жилого дома», то эта ошибка первого рода повлечет материальный ущерб; если же принято неправильное решение «продолжать строительство», несмотря на опасность обвала стройки, то эта ошибка второго рода может повлечь гибель людей. Можно привести примеры, когда ошибка первого рода влечет более тяжелые последствия, чем ошибка второго рода. Замечание 1. Правильное решение может быть принято также в двух случаях:
Замечание 2. Вероятность совершить ошибку первого рода принято обозначать через α; ее называют уровнем значимости. Наиболее часто уровень значимости принимают равным 0,05 или 0,01. Если, например, принят уровень значимости, равный 0,05, то это означает, что в пяти случаях из ста имеется риск допустить ошибку первого рода (отвергнуть правильную гипотезу).
2 вопрос. Статистический критерий проверки нулевой гипотезы. Наблюдаемое значение критерия. Для проверки нулевой гипотезы используют специально подобранную случайную величину, точное или приближенное распределение которой известно. Эту величину обозначают через U или Z, если она распределена нормально, F или υ2 - по закону Фишера-Снедекора, Т - по закону Стьюдента, χ2 - по закону «хи квадрат» и т. д. Поскольку в этом вид распределения во внимание приниматься не будет, обозначим эту величину в целях общности через К. Статистическим критерием (или просто критерием) называют случайную величину К, которая служит для проверки нулевой гипотезы. Например, если проверяют гипотезу о равенстве дисперсий двух нормальных генеральных совокупностей, то в качестве критерия К принимают отношение исправленных выборочных дисперсий: F = s21 / s22. Эта величина случайная, потому что в различных опытах дисперсии принимают различные, наперед неизвестные значения, и распределена по закону Фишера-Снедекора. Для проверки гипотезы по данным выборок вычисляют частные значения входящих в критерий величин и таким образом получают частное (наблюдаемое) значение критерия. Наблюдаемым значением Кнабл называют значение критерия, вычисленное по выборкам. Например, если по двум выборкам найдены исправленные выборочные дисперсии s21 = 20 и s22 = 5, то наблюдаемое значение критерия F Fнабл = s21 / s22 = 20 / 5 = 4.
Если закон распределения неизвестен, но есть основания предположить, что он имеет определенный вид (назовем его А), то проверяют нулевую гипотезу: генеральная совокупность распределена по закону А. Проверка гипотезы о предполагаемом законе неизвестного распределения производится так же, как и проверка гипотезы о параметрах распределения, т. е. при помощи специально подобранной случайной величины - критерия согласия. Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения. Имеется несколько критериев согласия: χ2 («хи квадрат») К. Пирсона, Колмогорова, Смирнова и др. Ограничимся описанием применения критерия Пирсона к проверке гипотезы о нормальном распределении генеральной совокупности (критерий аналогично применяется и для других распределений, в этом состоит его достоинство). С этой целью будем сравнивать эмпирические (наблюдаемые) и теоретические (вычисленные в предположении нормального распределения) частоты. Обычно эмпирические и теоретические частоты различаются. Случайно ли расхождение частот? Критерий Пирсона отвечает на поставленный выше вопрос. Правда, как и любой критерий, он не доказывает справедливость гипотезы, а лишь устанавливает на принятом уровне значимости ее согласие или несогласие с данными наблюдений. Итак, пусть по выборке объема n получено эмпирическое распределение:
Допустим, что в предположении нормального распределения генеральной совокупности вычислены теоретические частоты n'i. При уровне значимости α требуется проверить нулевую гипотезу: генеральная совокупность распределена нормально. В качестве критерия проверки нулевой гипотезы примем случайную величину
Эта величина случайная, так как в различных опытах она принимает различные, заранее не известные значения. Ясно, что чем меньше различаются эмпирические и теоретические частоты, тем меньше величина критерия (*), и, следовательно, он в известной степени характеризует близость эмпирического и теоретического распределений. Доказано, что при n→∞ закон распределения случайной величины (*) независимо от того, какому закону распределения подчинена генеральная совокупность, стремится к закону распределения χ2 с k степенями свободы. Поэтому случайная величина (*) обозначена через χ2, а сам критерий называют критерием согласия «хи квадрат». Число степеней свободы находят по равенству k = s-1-r, где s - число групп (частичных интервалов) выборки; r - число параметров предполагаемого распределения, которые оценены по данным выборки. В частности, если предполагаемое распределение - нормальное, то оценивают два параметра (математическое ожидание и среднее квадратическое отклонение), поэтому r = 2 и число степеней свободы k = s - 1 - r = s - 1 - 2 = s - 3. Поскольку односторонний критерий более «жестко» отвергает нулевую гипотезу, чем двусторонний, построим правостороннюю критическую область, исходя из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости α:
Таким образом, правосторонняя критическая область определяется неравенством χ2 > χ2 кр(α;k), а область принятия нулевой гипотезы - неравенством χ2 < χ2 кр(α;k). Обозначим значение критерия, вычисленное по данным наблюдений, через χ2набл и сформулируем правило проверки нулевой гипотезы. Правило. Для того чтобы при заданном уровне значимости проверить нулевую гипотезу H0: генеральная совокупность распределена нормально, надо сначала вычислить теоретические частоты, а затем наблюдаемое значение критерия:
и по таблице критических точек распределения по заданному уровню значимости α и числу степеней свободы k = s - 3 найти критическую точку χ2 кр(α;k). Если χ2 < χ2 кр - нет оснований отвергнуть нулевую гипотезу. Если χ2 > χ2 кр - нулевую гипотезу отвергают. Замечание 1. Объем выборки должен быть достаточно велик, во всяком случае ,не менее 50. Каждая группа должна содержать не менее 5 - 8 вариант; малочисленные группы следует объединять в одну, суммируя частоты. Замечание 2. Поскольку возможны ошибки первого и второго рода, в особенности если согласование теоретических и эмпирических частот «слишком хорошее», следует проявлять осторожность. Например, можно повторить опыт, увеличить число наблюдений, воспользоваться другими критериями, построить график распределения, вычислить асимметрию и эксцесс. Замечание 3. Для контроля вычислений формулу (**) преобразуют к виду
Пример. При уровне значимости 0,05 проверить гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические и теоретические частоты:
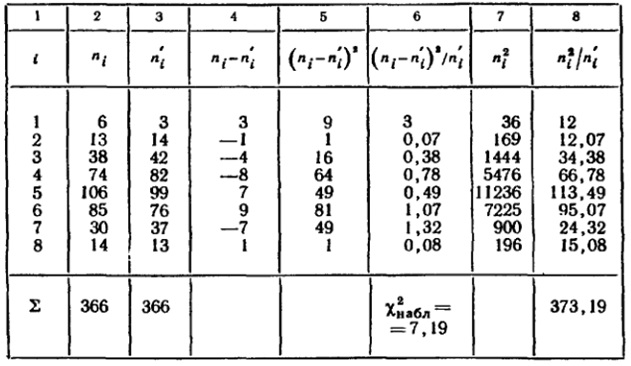
Решение. Вычислим χ2набл, для чего составим расчетную табл.
Контроль: χ2набл = 7,19
Вычисления произведены правильно. Найдем число степеней свободы, учитывая, что число групп выборки (число различных вариант) s = 8; k = 8-3 = 5. По таблице критических точек распределения χ2 (см. приложение 5), по уровню значимости α = 0,05 и числу степеней свободы k = 5 находим χ2 кр(0,05;5) = 11,1. Так как χ2набл < χ2 кр - нет оснований отвергнуть нулевую гипотезу. Другими словами, расхождение эмпирических и теоретических частот незначимое. Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности. | |||||||||||||||||||||||||||||
| Категория: Лекции | Просмотров: 1902 | |||||||||||||||||||||||||||||
| Всего комментариев: 0 | |
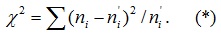 . (*)
. (*)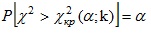
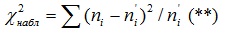 (**)
(**)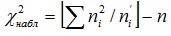 .
.
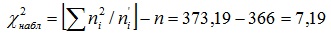 .
.