| Главная » Статьи » Лекции |
|
2 вопрос. Локальная теорема Лапласа. 3 вопрос. Интегральная теорема Лапласа.
Если производится несколько испытаний, причем вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А. Будем рассматривать независимые испытания, в которых событие А имеет одну и туже вероятность. Сложным событием называется совмещение нескольких отдельных событий, которые называют простыми. Пусть производится n независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Условимся считать, что вероятность события А в каждом испытании одна и та же, а именно равна р. Следовательно, вероятность ненаступления события А в каждом испытании так же постоянна и равна q = 1 - p . Вычислить вероятность того, что при n испытаниях событие А осуществится ровноkраз и, следовательно, не осуществится ровно n-k раз. Поставленную задачу можно решить с помощью так называемой формулы Бернулли. Вывод формулы Бернулли. Вероятность одного сложного события, состоящего в том, что в n испытаниях событие А наступит k раз и не наступит n-k раз, по теореме умножения вероятностей независимых событий равна pkqn-k . Таких сложных событий может быть столько, сколько можно составить сочетаний из n элементов по k элементов, т.е.Ckn . Так как эти сложные события несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме вероятностей всех возможных сложных событий. Поскольку же вероятности всех этих сложных событий одинаковы, то искомая вероятность (появления k раз события А в n испытаниях) равна вероятности одного сложного события, умноженной на их число:
или
Полученную формулу называют формулой Бернулли.
Пример. Вероятность того, что расход электроэнергии в продолжение одних суток не превысит установленной нормы, равна p=0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы. Решение. Вероятность нормального расхода электроэнергии в продолжение каждых из 6 суток постоянна и равна p=0,75. Следовательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна q = 1 - p = 1 -0,75 = 0,25 Искомая вероятность по формуле Бернулли равна
Вероятность того, что в n испытаниях событие наступит: а) менее k раз P = Pn (0) + Pn(1) + ... + Pn(k-1) б) более k раз P = Pn (k+1) + Pn(k+2) + ... + Pn(n) в) не менее k раз P = Pn (k) + Pn(k+1) + ... + Pn(k) г) не более k раз P = Pn (0) + Pn(1) + ... + Pn(k)
2 вопрос. Локальная теорема Лапласа. Пользоваться формулой Бернулли при больших значениях n достаточно трудно, так как формула требует выполнения действий над громадными числами.
Например, если n=50, k=30, p=0,1, то для отыскания вероятности P50(30) надо вычислить выражение
где 50! = 30414093 · 1057 30! = 26525286 · 1025 20! = 24329020 · 1011
Локальная теорема Лапласа дает асимптотическую формулу, которая позволяет приближенно найти вероятность появления события ровно k раз в n испытаниях, если число испытаний достаточно велико. Заметим, что для частного случая, а именно для р=1/2 асимптотическая формула была найдена в 1730 г. Муавром; в 1783 г. Лаплас обобщил формулу Муавра для произвольного р, отличного от 0 и 1. Поэтому теорему, иногда называют теоремой Муавра-Лапласа. Локальная теорема Лапласа. Если вероятность появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Pn(k) того, что событие А появится в n испытаниях ровно k, приближенно равна (тем точнее, чем больше n) значению функции
при
Имеются таблицы, в которых помещены значения функции Вероятность того, что событие А появится в n независимых испытаниях, ровно k раз, приближенно равна
где
Пример. Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2. Решение. По условию n=400; k=80; p=0,2; q=1-p=0,8. Воспользуемся асимптотической формулой Лапласа:
Вычислим определяемое данными задачи значение x:
По таблице приложения 1 находим Искомая вероятность
3 вопрос. Интегральная теорема Лапласа. Производится n испытаний, в каждом из которых вероятность появления события А постоянна и равна р (0 < р < 1). Вычислить вероятность Pn(k1, k2) того, что событие А появится в n испытаниях не менее k1 и не более k2 раз (для краткости говорят «от k1 до k2 раз»). На этот вопрос отвечает интегральная теорема Лапласа. Интегральная теорема Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Pn(k1, k2) того, что событие А появится в п испытаниях от k1 до k2 раз, приближенно равна определенному интегралу
где
При решении задач, требующих применения интегральной теоремы Лапласа, пользуются специальными таблицами, так как неопределенный интеграл Для того чтобы можно было пользоваться таблицей функции Лапласа, преобразуем соотношение (2.26) так:
Итак вероятность того, что событие А появится в n независимых испытаниях от k1 до k2 раз,
где
Пример. Вероятность того, что деталь не прошла проверку ОТК, равна р=0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей. Решение. По условию p=0,2; q=1-p=0,8; n=400; k1=70; k2=100. Воспользуемся интегральной теоремой Лапласа:
Вычислим нижний и верхний пределы интегрирования:
Таким образом, имеем P400(70;100) = Ф(2,5) - Ф(-1,25) = Ф(2,5) + Ф(1,25) По таблице приложения находим: Ф(2,5) = 0,4938; Ф(1,25) = 0,3944. Искомая вероятность P400(70;100) = 0,4938 + 0,3944 = 0,8882
| |
| Категория: Лекции | Просмотров: 1036 | |
| Всего комментариев: 0 | |
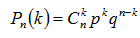 (2.22)
(2.22)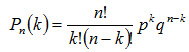 .(2.23)
.(2.23)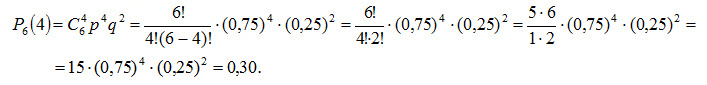
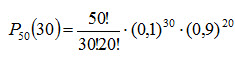
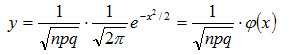 (2.24)
(2.24)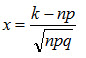
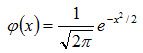 соответствующие положительным значениям аргумента x (см. приложение 1). Для отрицательных значений аргумента пользуются теми же таблицами, так как функция
соответствующие положительным значениям аргумента x (см. приложение 1). Для отрицательных значений аргумента пользуются теми же таблицами, так как функция 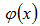 четна, т.е.
четна, т.е. 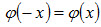 .
.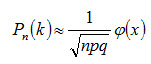 (2.25)
(2.25)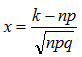
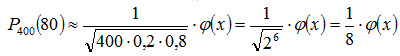 .
. .
.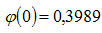 .
.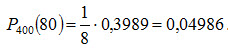 .
.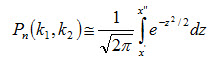 , (2.26)
, (2.26)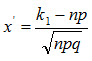 и
и 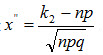 .
.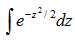 не выражается через элементарные функции. Имеются таблицы для интеграла
не выражается через элементарные функции. Имеются таблицы для интеграла 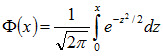 (см. приложение 2). В таблице даны значения функции Ф(x) для положительных значений x и x=0; для x<0 пользуются той же таблицей. Функция Ф(x) нечетна, т.е. Ф(-x) = - Ф(x) . В таблице приведены значения интеграла лишь до x=5, так как для x>5 можно принять Ф(x) = 0,5 . Функцию Ф(x) часто называют функцией Лапласа.
(см. приложение 2). В таблице даны значения функции Ф(x) для положительных значений x и x=0; для x<0 пользуются той же таблицей. Функция Ф(x) нечетна, т.е. Ф(-x) = - Ф(x) . В таблице приведены значения интеграла лишь до x=5, так как для x>5 можно принять Ф(x) = 0,5 . Функцию Ф(x) часто называют функцией Лапласа.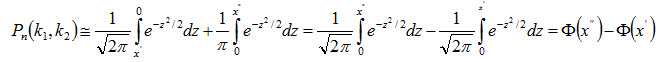 .
.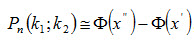 , (2.27)
, (2.27)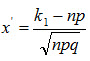 и
и 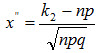 .
.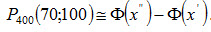 .
.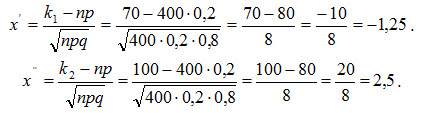 ..
..