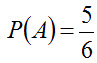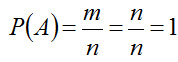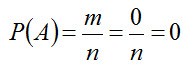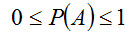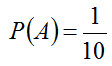| Главная » Статьи » Лекции |
1 вопрос. Классификация событий. 2 вопрос. Виды случайных событий. 3 вопрос. Классическое определение вероятности.
1 вопрос. Классификация событий. Одним из основных понятий теории вероятностей является понятие события. Наблюдаемые нами события (явления) можно подразделить на следующие три вида:
Достоверным называют событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий S.
Пример 1. Если в сосуде содержится вода при нормальном атмосферном давлении и температуре 20°, то событие «вода в сосуде находится в жидком состоянии» есть достоверное. В этом примере заданные атмосферное давление и температура воды составляют совокупность условий S.
Невозможным называют событие, которое заведомо не произойдет, если будет осуществлена совокупность условий S.
Пример 2. Событие «вода в сосуде находится в твердом состоянии» заведомо не произойдет, если будет осуществлена совокупность условий примера 1.
Случайным называют событие, которое при испытании может либо произойти, либо не произойти.
Пример 3. Если брошена монета, то она может упасть так, что сверху будет либо герб, либо надпись.
Под испытанием понимается выполнение определенного комплекса условий, в которых наблюдается то или иное явление, фиксируется тот или иной результат. Испытание может быть осуществлено человеком, но может проводиться и независимо от человека, выступающего в этом случае в роли наблюдателя. Событие — это результат испытания. События обозначаются прописными (заглавными) буквами латинского алфавита: А, В, С.
Пример 4. Стрелок стреляет по мишени» разделенной на четыре области. Выстрел—это испытание. Попадание в определенную область мишени — событие. Пример 5. В урне имеются цветные шары. Из урны наудачу берут один шар. Извлечение шара из урны есть испытание. Появление шара определенного цвета — событие.
2 вопрос. Виды случайных событий. События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.
Пример 1. Из ящика с деталями наудачу извлечена деталь. Появление стандартной детали исключает появление нестандартной детали. События «появилась стандартная деталь» и «появилась нестандартная деталь» — несовместные. Пример 2. Брошена монета. Появление «герба» исключает появление надписи. События «появился герб» и «появилась надпись» — несовместные. Пример 3. Выигрыш по одному билету денежно-вещевой лотереи двух ценных предметов – события несовместные. Пример 4. Получение студентом на экзамене по одной дисциплине оценок «отлично», «хорошо» и «удовлетворительно» - события несовместные. Несколько событий образуют полную группу, если в результате испытания появится хотя бы одно из них. Другими словами, появление хотя бы одного из событий полной группы есть достоверное событие. Пример 5. События, состоящие в том, что в семье из двух детей: А – «два мальчика», В – «один мальчик, одна девочка», С – «две девочки». События А, В, С образуют полную группу.
В частности, если события, образующие полную группу, попарно несовместны, то в результате испытания появится одно и только одно из этих событий.
Пример 6. Приобретены два билета денежно-вещевой лотереи. Обязательно произойдет одно и только одно из следующих событий: «выигрыш выпал на первый билет и не выпал на второй», «выигрыш не выпал на первый билет и выпал на второй», «выигрыш выпал на оба билета», «на оба билета выигрыш не выпал». Эти события образуют полную группу попарно несовместных событий. Пример 7. Стрелок произвел выстрел по цели. Обязательно произойдет одно из следующих двух событий: попадание, промах. Эти два несовместных события образуют полную группу.
События называют равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое.
Пример 8. Появление «герба» и появление надписи при бросании монеты — равновозможные события. Действительно, предполагается, что монета изготовлена из однородного материала, имеет правильную цилиндрическую форму и наличие чеканки не оказывает влияния на выпадение той или иной стороны монеты. Пример 9. Появление того или иного числа очков на брошенной игральной кости — равновозможные события. Действительно, предполагается, что игральная кость изготовлена из однородного материала, имеет форму правильного многогранника и наличие очков не оказывает влияния на выпадение любой грани.
Два несовместных события, из которых одно должно обязательно произойти, называются противоположными. Событие, противоположное событию А, обозначается
Пример 10. Появление «герба» и появление «решки» при подбрасывании монеты - события противоположные. Пример 11. Отсутствие бракованных изделий и «наличие хотя бы одного бракованного изделия» в партии - события противоположные.
3 вопрос. Классическое определение вероятности. Вероятность — одно из основных понятий теории вероятностей. Вероятность есть число, характеризующее степень возможности появления события. Каждый из возможных результатов испытания называется элементарным исходом (элементарным событием). Элементарные исходы обозначаются через ωi. Те элементарные исходы, в которых интересующее нас событие наступает, называются благоприятствующими этому событию. Согласно классическому определению вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу, т.е.
где P(A) – вероятность события A, m – число элементарных исходов, благоприятствующих A, n - число всех возможных элементарных исходов испытания.
Предполагается, что элементарные исходы несовместны, равновозможны и образуют полную группу.
Пример 1. Пусть в урне содержится 6 одинаковых, тщательно перемешанных шаров, причем 2 из них — красные, 3—синие и 1—белый. Какова вероятность вынуть наудачу из урны цветной шар (красный или синий)? Решение. Появление цветного шара будем рассматривать в качестве события А. Испытание состоит в извлечении шара из урны. В нашем примере возможны следующие 6 элементарных исходов: ω1 — появился белый шар; ω2, ω3 —- появился красный шар; ω4, ω5, ω6 —появился синий шар. Эти исходы образуют полную группу попарно несовместных событий (обязательно появится только один шар) и они равновозможны (шар вынимают наудачу, шары одинаковы и тщательно перемешаны). В нашем примере благоприятствуют событию А (появлению цветного шара) следующие 5 исходов: ω2, ω3, ω4, ω5, ω6. Событие А наблюдается, если в испытании наступит ω2 или ω3, или ω4, или ω5, или ω6. В этом смысле событие А подразделяется на несколько элементарных событий (ω2, ω3, ω4, ω5, ω6); элементарное же событие не подразделяется на другие события. В этом состоит различие между событием А и элементарным событием (элементарным исходом). Всего элементарных исходов 6 (n=6); из них 5 благоприятствуют событию А. Следовательно, вероятность того, что взятый шар окажется цветным, равна
Свойства вероятности события. Свойство 1. Вероятность достоверного события равна единице, т.е. P (A) = 1 Действительно, если событие достоверно, то каждый элементарный исход испытания благоприятствует событию. В этом случае m = n , следовательно,
Свойство 2. Вероятность невозможного события равна нулю, т.е. P (A) = 0 Действительно, если событие невозможно, то ни один из элементарных исходов испытания не благоприятствует событию. В этом случае m = 0 , следовательно,
Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей, т.е.
Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания. В этом случае 0 < m < n , значит,
следовательно, 0 < P(A) < 1
Пример 2. Набирая номер телефона, абонент забыл одну цифру и набрал ее наудачу. Найти вероятность того, что набрана нужная цифра. Решение. Обозначим через А событие – набрана нужная цифра. Абонент мог набрать любую из 10 цифр, поэтому общее число возможных элементарных исходов равно 10. Эти исходы несовместны, равномозможны и образуют полную группу. Благоприятствует событию А лишь один исход (нужная цифра лишь одна). Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:
| |
| Категория: Лекции | Просмотров: 1483 | |
| Всего комментариев: 0 | |
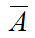 .
.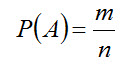 (2.1)
(2.1)