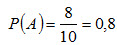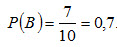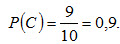| Главная » Статьи » Лекции |
1 вопрос. Теорема сложения вероятностей несовместных событий. 2 вопрос.Условная вероятность. 3 вопрос.Теорема умножения вероятностей. 4 вопрос.Независимые события. Теорема умножения для независимых событий.
1 вопрос. Теорема сложения вероятностей несовместных событий. Суммой А + В двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий. Пример 1. Если из орудия произведены два выстрела и А — попадание при первом выстреле, В — попадание при втором выстреле, то А + В — попадание при первом выстреле, или при втором, или в обоих выстрелах.
В частности, если два события А и В — несовместные, то А + В — событие, состоящее в появлении одного из этих событий, безразлично какого. Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного из этих событий.
Пример 2. Событие А + В + С состоит в появлении одного из следующих событий: А, В, С, А и В, А и С, В и С, А и В и С.
Пусть события А и В — несовместные, причем вероятности этих событий известны. Теорема сложения. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
Следствие. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
Пример 3. В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара. Решение. Появление цветного шара означает появление либо красного, либо синего шара. Вероятность появления красного шара (событие А)
Вероятность появления синего шара (событие В)
События А и В несовместны (появление шара одного цвета исключает появление шара другого цвета), поэтому теорема сложения применима. Искомая вероятность
Теорема 1. Сумма вероятностей событий А1,А2, …, Ап, образующих полную группу, равна единице:
Пример 4. Консультационный пункт института получает пакеты с контрольными работами из городов A, B и C. Вероятность получения пакета из города А равна 0,7, из города В —0,2. Найти вероятность того, что очередной пакет будет получен из города С. Решение. События «пакет получен из города A», «пакет получен из города В», «пакет получен из города С» образуют полную группу, поэтому сумма вероятностей этих событий равна единице: 0,7 + 0,2 + p = 1 Отсюда искомая вероятность p = 1 - 0,9 = 0,1
Теорема 2. Сумма вероятностей противоположных событий равна единице:
Замечание 1. Если вероятность одного из двух противоположных событий обозначена через р, то вероятность другого события обозначают черезq.Таким образом, в силу предыдущей теоремы (2.5) p + q = 1
Пример 5. Вероятность того, что день будет дождливым, р = 0,7. Найти вероятность того, что день будет ясным. Решение. События «день дождливый» и «день ясный» - противоположные, поэтому искомая вероятность q = 1 - p = 1 - 0,7 = 0,3
2 вопрос. Условная вероятность. Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий.
Пример 1. Если А — деталь годная, В — деталь окрашенная, то АВ — деталь годна и окрашена.
Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий.
Пример 2. Если А, В, С появление «герба» соответственно в первом, втором и третьем бросаниях монеты, то ABC— выпадение «герба» во всех трех испытаниях.
Вероятность называют безусловной если при вычислении вероятности события никаких других ограничений, кроме условий S (совокупности условий S), не налагается. Если же налагаются и другие дополнительные условия, товероятность события называют условной. Например, часто вычисляют вероятность события В при дополнительном условии, что произошло событие А. Заметим, что и безусловная вероятность, строго говоря, является условной, поскольку предполагается осуществление условий S. Условной вероятностью РА(В) называют вероятность события В, вычисленную в предположении, что событие А уже наступило. Условная вероятность события В при условии, что событие А уже наступило, по определению, равна
Пример 3. В урне 3 белых и 3 черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно. Найти вероятность появления белого шара при втором испытании (событие В), если при первом испытании был извлечен черный шар (событие А). Решение. Вероятность появления белого шара при первом испытании
Найдем вероятность Р(АВ) того, что в первом испытании появился черный шар, а во втором – белый. Общее число исходов – совместного появления двух шаров, безразлично какого цвета, равно числу размещений A26 = 6 · 5 = 30 . Из этого числа исходов событию AB благоприятствуют 3 · 3 = 9 исходов. Следовательно,
Искомая условная вероятность
3 вопрос. Теорема умножения вероятностей. Рассмотрим два события: А и В; пусть вероятности Р(А) и РА(В) известны. Теорема умножения. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
Замечание.
Следствие. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились.
где
Пример 1. У сборщика имеется 3 конусных и 7 эллиптических валиков. Сборщик взял один валик, а затем второй. Найти вероятность того, что первый из взятых валиков — конусный, а второй — эллиптический. Решение. Вероятность того, что первый валик окажется конусным (событие А),
Вероятность того, что второй валик окажется эллиптическим (событие B), вычисленная в предположении, что первый валик— конусный, т.е. условная вероятность
По теореме умножения, искомая вероятность
Заметим, что, сохранив обозначения, легко найдем:
что наглядно иллюстрирует справедливость равенства (2.8).
4 вопрос.Независимые события. Теорема умножения для независимых событий. Пусть вероятность события В не зависит от появления события А. Событие В называют независимым от события А, если появление события А не изменяет вероятности события В, т.е. если условная вероятность события В равна его безусловной вероятности:
Тогда Если событие В не зависит от события А, то и событие А не зависит от события В; это означает, что свойство независимости событий взаимно.
Теорема умножения для независимых событий. Вероятность совместного появления двух независимых событий равна произведению вероятности этих событий, т.е.
Равенство (2.11) принимают в качестве определения независимых событий. Два события называют независимыми, если вероятность их совмещения равна произведению вероятностей этих событий, в противном случае события называют зависимыми.
Пример 1. Найти вероятность совместного поражения цели двумя орудиями, если вероятность поражения цели первым орудием (событие А) равна 0,8, а вторым (событие В) – 0,7. Решение. События А и В независимые, поэтому, по теореме умножения, искомая вероятность
Несколько событий называют попарно независимыми, если каждые два из них независимы. Например, события А, В, С попарно независимы, если независимы события А и В, А и С, В и С.
Несколько событий называют независимыми в совокупности (или просто независимыми), если независимы каждые два из них и независимы каждое событие и все возможные произведения остальных. Например, если события А1, А2, А3 независимы в совокупности, то независимы события А1 и А2, А1 и А3, А2 и А3, А1 и А2А3, А2 и А1А3, А3 и А1А2.
Следствие. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий: P(А1 А2 ...An) = P(А1) P(А2) ...P(Аn) (2.12) Замечание. Если события А1, А2, …, Аn независимы в совокупности, то и противоположные им события Пример 2. Имеется 3 ящика, содержащих по 10 деталей. В первом ящике 8, во втором 7 и в третьем 9 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что три вынутые детали окажутся стандартными. Решение. Вероятность того, что из первого ящика вынута стандартнаядеталь (событие А),
Вероятность того, что из второго ящика вынута стандартная деталь (событие В),
Вероятность того, что из третьего ящика вынута стандартная деталь (событие С),
Так как события А, В и С независимые в совокупности, то искомая вероятность (по теореме умножения) равна P(АВС) = P(A)· P(B)· P(C) = 0,8 · 0,7 · 0, 9 = 0,504 | |
| Категория: Лекции | Просмотров: 2137 | |
| Всего комментариев: 0 | |
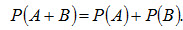 (2.2)
(2.2)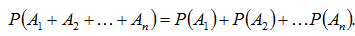 (2.3)
(2.3)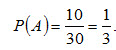
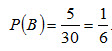
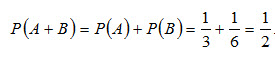
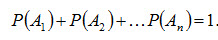 (2.4)
(2.4)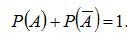 (2.5)
(2.5)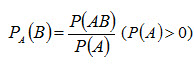 (2.6)
(2.6)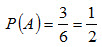
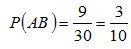
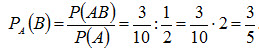
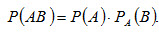 (2.7)
(2.7)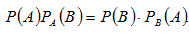 (2.8)
(2.8)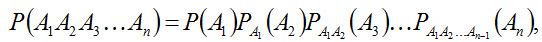 (2.9)
(2.9)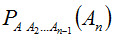 — вероятность события Аn, вычисленная в предположении, что события А1,А2, ...,Ап-1 наступили.
— вероятность события Аn, вычисленная в предположении, что события А1,А2, ...,Ап-1 наступили.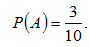
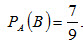
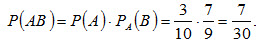
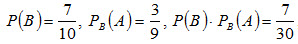
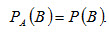 (2.10)
(2.10)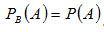 .
.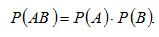 (2.11)
(2.11)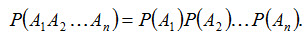
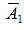 ,
,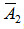 , …
, … 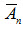 также независимы в совокупности.
также независимы в совокупности.