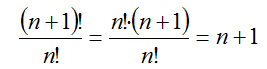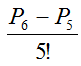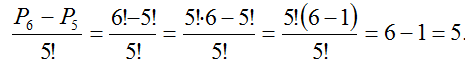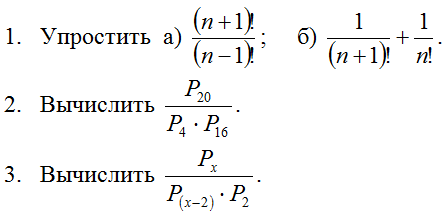| Главная » Статьи » Лекции |
1 вопрос. Предмет теории вероятностей и математической статистики. 2 вопрос. Понятия комбинаторики и факториала.
1 вопрос. Предмет теории вероятностей и математической статистики. Задача любой науки, в том числе экономической, состоит в выявлении и исследовании закономерностей, которым подчиняются реальные процессы. Найденные закономерности, относящиеся к экономике, имеют не только теоретическую ценность, они широко применяются на практике — в планировании, управлении и прогнозировании. Теория вероятностей — математическая наука, изучающая закономерности случайных явлений. Под случайными явлениями понимаются явления с неопределенным исходом, происходящие при неоднократном воспроизведении определенного комплекса условий. Математическая статистика — раздел математики, изучающий математические методы сбора, систематизации, обработки и интерпретации результатов наблюдений с целью выявления статистических закономерностей. Математическая статистика опирается на теорию вероятностей. Если теория вероятностей изучает закономерности случайных явлений на основе абстрактного описания действительности (теоретической вероятностной модели), то математическая статистика оперирует непосредственно результатами наблюдений над случайным явлением, представляющими выборку из некоторой конечной или гипотетической бесконечной генеральной совокупности. Используя результаты, полученные теорией вероятностей, математическая статистика позволяет не только оценить значения искомых характеристик, но и выявить степень точности получаемых при обработке данных выводов. Если говорить кратко, теория вероятностей позволяет находить вероятности «сложных» событий через вероятности «простых» событий (связанных с ними каким-либо образом), а математическая статистика по наблюденным значениям (выборке) оценивает вероятности этих событий либо осуществляет проверку предположений (гипотез) относительно этих вероятностей. Изучение вероятностных моделей дает возможность понять различные свойства случайных явлений на абстрактном и обобщенном уровне, не прибегая к эксперименту. В математической статистике, наоборот, исследование связано с конкретными данными и идет от практики (наблюдения) к гипотезе и ее проверке.
2 вопрос. Понятия комбинаторики и факториала. Для успешного решения задач с использованием классического определения вероятности необходимо знать основные правила и формулы комбинаторики – раздела математики, изучающего в частности, методы решения комбинаторных задач – задач на подсчет числа различных комбинаций. В разделе математики, который называется комбинаторикой, решаются некоторые задачи, связанные с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств. Например, если взять 10 различных цифр 0, 1, 2, 3, ..., 9 и составлять из них комбинации, то будем получать различные числа, например, 345, 534, 1036, 5671, 45 и т. п. Мы видим, что некоторые из таких комбинаций отличаются только порядком цифр (например, 345 и 534), другие — входящими в них цифрами (например, 1036 и 5671), третьи различаются и числом цифр (например, 345 и 45). Таким образом, полученные комбинации удовлетворяют различным условиям. В зависимости от правил составления можно выделить три типа комбинаций: перестановки, размещения, сочетания. Предварительно познакомимся с понятием факториала. Произведение всех натуральных чисел от 1 до п включительно называют п-факториалом и пишут n!=1·2·3·...(n-1)·n Заметим, что удобно рассматривать 0!, полагая, по определению, 0!=1.
1. Вычислить: а) 3!; б) 7!-5!; в) (7!+5!)/6!. Решение. а) 3! = 1·2·3 = 6 б) Так как 7! = 1·2·3·4·5·6·7 и 5! = 1·2·3·4·5, то можно вынести за скобки 5!. Тогда получим 7!-5! = 5!·(6·7-1) = 5!·41 = 1·2·3·4·5·41 = 4920. в) 2. Упростить Решение. Учитывая, что (n+1)! = 1·2·3·...·n·(n+1) = n!·(n+1), а n! = 1·2·3·...(n-1)·n, сократим дробь:
Пусть даны три буквы А, В, С. Составим все возможные комбинации из этих букв: ABC; АСВ; ВСА; CAB; СВА; ВАС (всего 6 комбинаций). Мы видим, что они отличаются друг от друга только порядком расположения букв. Комбинации из п элементов, которые отличаются друг от друга только порядком элементов, называются перестановками. Перестановки обозначаются символом Рn, где п — число элементов, входящих в каждую перестановку. Число перестановок можно вычислить по формуле Pn = n·(n - 1)·(n - 2)...·3·2·1 (1.1) или с помощью, факториала: Pn = n! (1.2) Так, число перестановок из трех элементов согласно формуле (2) составляет P3 = 3! = 3·2·1 = 6, что совпадает с результатом рассмотренного выше примера. Действительно, на первое место в комбинации (перестановке) можно поставить три буквы. На второе место уже можно поставить только две буквы из трех (одна заняла первое место), а на третьем окажется только одна из оставшихся. Значит, 3·2·1 = 6 = P3.
3. Сколько различных пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5 при условии, что ни одна цифра в числе не повторяется? P5 = 5! = 1·2·3·4·5 = 120. 4. В соревнованиях участвовало четыре команды. Сколько вариантов распределения мест между ними возможно? P4 = 4! = 1·2·3·4·5 = 24.
5. Вычислить Решение. Учитывая, что P6 = 6!, а P5 = 5!, сократим дробь:
| |
| Категория: Лекции | Просмотров: 1076 | |
| Всего комментариев: 0 | |
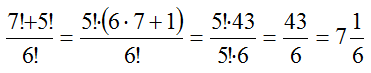
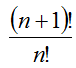 .
.