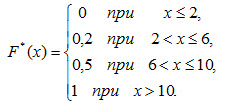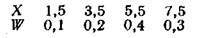| Главная » Статьи » Лекции |
|
1 вопрос. Задачи математической статистики. 2 вопрос. Генеральная и выборочная совокупность. 3 вопрос. Виды выборок и способы отбора. Часть 2 4 вопрос. Статистическое распределение выборки. 5 вопрос. Эмпирическая функция распределения. 6 вопрос. Полигон и гистограмма.
4 вопрос. Статистическое распределение выборки. Пусть из генеральной совокупности извлечена выборка, причем х1 наблюдалось n1 раз, х2 - п2 раз, хk - пk раз и Σпi=п - объем выборки. Наблюдаемые значения хi называют вариантами, а последовательность вариант, записанных в возрастающем порядке,— вариационным рядом. Числа наблюдений называют частотами, а их отношения к объему выборки ni/n = Wi — относительными частотами. Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот. Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал). Заметим, что в теории вероятностей под распределением понимают соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике — соответствие между наблюдаемыми вариантами и их частотами, или относительными частотами.
Пример. Задано распределение частот выборки объёма n = 20:
Написать распределение относительных частот. Решение. Найдем относительные частоты, для чего разделим частоты на объем выборки:
Напишем распределение относительных частот:
Контроль: 0,15 + 0,50+0,35=1.
5 вопрос. Эмпирическая функция распределения. Эмпирической функцией распределения (функцией распределения выборки) называют функцию F*(x), определяющую для каждого значения х относительную частоту события X < х:
где пх — число вариант, меньших х; п — объем выборки.
В отличие от эмпирической функции распределения выборки функцию распределения F(х) генеральной совокупности называют теоретической функцией распределения. Различие между эмпирической (опытной) и теоретической функциями состоит в том, что теоретическая функция F(х) определяет вероятность события X < х, а эмпирическая функция F*(х) определяет относительную частоту этого же события. При больших п числа F*(х) и F(х) мало отличаются одно от другого в том смысле, что
Уже отсюда следует целесообразность использования эмпирической функции распределения выборки для приближенного представления теоретической (интегральной) функции распределения генеральной совокупности. F*(х) обладает всеми свойствами F(x). Действительно, из определения функции F*(х) вытекают следующие ее свойства:
Итак, эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.
Пример. Построить эмпирическую функцию по данному распределению выборки:
Решение. Найдем объем выборки: 12 + 18 + 30 = 60. Наименьшая варианта равна 2, следовательно,
Значение X < 6, а именно x1 = 2, наблюдается 12 раз, следовательно,
Значение X < 10, а именно x1 = 2 и x2 = 6, наблюдалось 12 + 18 = 30 раз, следовательно,
Так как x = 10 - наибольшая варианта, то
Искомая эмпирическая функция
Построим график эмпирической функции распределения.
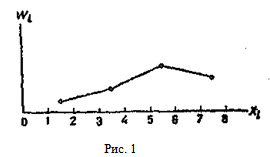
6 вопрос. Полигон и гистограмма. Для наглядности строят различные графики статистического распределения и, в частности, полигон и гистограмму. Полигоном частот называют ломаную, отрезки которой соединяют точки (х1; n1), (х2; n2),…, (хk; nk). Для построения полигона частот на оси абсцисс откладывают варианты хi, а на оси ординат — соответствующие им частоты ni. Точки (хi; ni) соединяют отрезками прямых и получают полигон частот. Полигоном относительных частот называют ломаную, отрезки которой соединяют точки (х1; W1), (х2; W2), ..., (хk; Wk). Для построения полигона относительных частот на оси абсцисс откладывают варианты хi, а на оси ординат — соответствующие им относительные частоты Wi. Точки (хi ; Wi) соединяют отрезками прямых и получают полигон относительных частот.
На рис. 1 изображен полигон относительных частот следующего распределения:
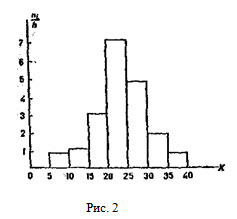
В случае непрерывного признака целесообразно строить гистограмму, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала пi — сумму частот вариант, попавших в i-й интервал. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, a высоты равны отношению ni/h (плотность частоты). Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии ni/h. Площадь i-го частичного прямоугольника равна hni/h = ni — сумме частот вариант i -го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т. е. объему выборки.
На рис. 2 изображена гистограмма частот распределения объема n=100, приведенного в табл. 1.
Таблица 1
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению Wi /h (плотность относительной частоты). Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии Wi/h. Площадь i-го частичного прямоугольника равна hWi/h= Wi — относительной частоте вариант, попавших в i-й интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т. е. единице. | |||||||||||||||||||||||||||||||
| Категория: Лекции | Просмотров: 532 | |||||||||||||||||||||||||||||||
| Всего комментариев: 0 | |
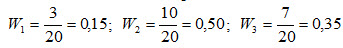
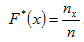 , (6.1)
, (6.1)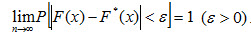 .
.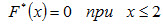 .
.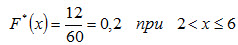 .
.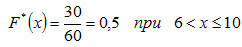 .
.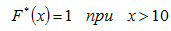 .
.