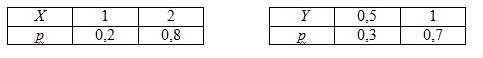| Главная » Статьи » Практика |
Цель работы: - научиться вычислять математическое ожидание, дисперсию и среднее квадратическое отклонение - научиться применять свойства математического ожидания и дисперсии Оснащенность: - калькулятор - раздаточный материал ЗАДАНИЯ
Пример 1. Найти математическое ожидание дискретной случайной величины, зная закон её распределения:
Пример 2. Дискретные независимые случайные величины заданы законами распределения:
Найти математическое ожидание произведения XY. Пример 3. Дан перечень возможных значений дискретной случайной величины X: х1 =-1, х2=0, х3=1, а также известны математические ожидания этой величины и ее квадрата: М (Х) = 0,1, М (Х2) = 0,9. Найти вероятности р1, р2, р3 соответствующие возможным значениям x1, x2, x3.
2.Дисперсия дискретной случайной величины. Пример 4. Найти дисперсию случайной величины, зная закон её распределения.
Пример 5. Случайная величина X может принимать два возможных значения: x1 с вероятностью 0,3 и x2 с вероятностью 0,7, причем х2 > х1. Найти х1 и х2, зная, что M (X) =2,7 и D (X) = 0,21.
3.Среднее квадратическое отклонение дискретной случайной величины. Пример 6. Случайная величина задана законом распределения
Найти среднее квадратическое отклонение этой величины. | |||||||||
| Категория: Практика | Просмотров: 991 | |||||||||
| Всего комментариев: 0 | |